
En primer lugar, comprobamos que el conjunto esté en equilibrio. Efectivamente:
450 - 275 - 175 = 0 N.m
Esto quiere decir que el eje o bien no se mueve, o bien gira con velocidad angular constante. De no haber sido así, el eje y sus ruedas se estarían acelerando, y los momentos en los tramos del eje serían distintos, influyendo en ellos la inercia de las ruedas.
Lo cierto es que la suma de momentos es cero, y podemos aplicar el modelo estático que hemos desarrollado. Cabe hacer la salvedad de que si el conjunto está girando con cierta velocidad angular, existe un efecto centrífugo que no estamos teniendo en cuenta, y que en todo caso consideraremos despreciable al menos en el eje (si en algún sitio es más verosímil esta hipótesis será en el eje, dado su menor diámetro). La conclusión de estas consideraciones es que el momento en el tramo 1-2 será de 275 T.m, y en el tramo 2-3 de 175 T.m.
Tramo 1-2. (Mx=275 N.m)

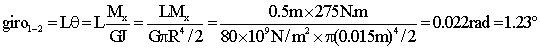
Tramo 2-3. (Mx=175 N.m)
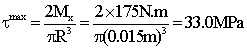
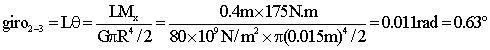
Las tensiones obtenidas son relativamente bajas, pensando que se trate de un eje de acero (el valor de G que da el enunciado es bastante típico de un acero), en el que las tensiones admisibles serían como poco 220MPa.
Aunque el enunciado no lo pide, es evidente que el giro relativo entre las ruedas 1 y 3 puede obtenerse por diferencia del giro de ambas con la rueda 2, es decir, 1.23-0.63=0.6º sería el ángulo de giro de la rueda 1 respecto de la 3 (vectorialmente hacia la derecha, sentido de AB).
![]()