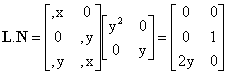
Las funciones dadas en el enunciado implican que la aproximación del campo de desplazamientos será de la forma:
ux = a1x N1x = a1x y2, para ux uy = a1y N1y = a1y y, para uy
Como en este caso solamente hay una función de aproximación por cada componente, obviaremos el subíndice 1 en los parámetros "a" y en las funciones "N". Escribiendo la aproximación en forma matricial, tenemos:
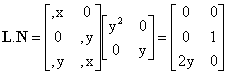
La matriz de rigidez resulta:
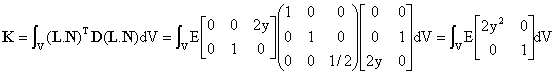
Siguiendo las pautas del enunciado, dividimos el dominio de integración en trozos rectangulares o triangulares, para integrar numéricamente. La manera mínima de hacerlo es con las dos divisiones mostradas en la figura:
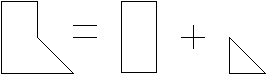
Por supuesto, cuanto más se subdivida, más exactamente se calculan las integrales. Realizando cuadratura de Gauss de un punto en cada subdominio, y sumando las aportaciones tenemos:

En donde la primera aportación corresponde al rectángulo (de área 2a2 y centro de gravedad en y=a) y la segunda al triángulo (de área a2/2 y centro de gravedad en y=a/3). Pasamos a calcular el término de cargas, que incluye una integral de volumen y otra de contorno:
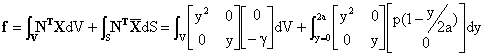
Para realizar la integral de volumen dividimos el dominio en dos trozos y procedemos como el el cálculo de la matriz de rigidez. Para realizar la integral de contorno, siendo el dominio de integración una línea, el enunciado nos permite no subdividir. El primer sumando de los siguientes corresponde a la integral de dominio en el rectángulo, el segundo en el triángulo, y el tercero a la integral de línea.
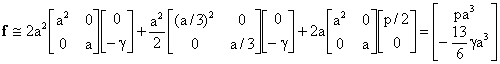
El sistema global de ecuaciones queda:
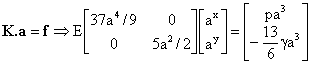
El sistema de ecuaciones anterior es inmediato de resolver:
![]()
Que es el campo de desplazamientos aproximado que se pide. Su forma indica que los puntos del sólido se mueven hacia abajo y hacia la derecha, como cabía esperar a la vista de las cargas.
Calculados los parámetros a, las tensiones aproximadas se obtienen como:
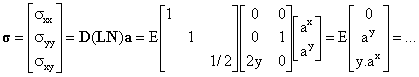
Un paréntesis de reflexión: la expresión anterior de las tensiones se podía haber escrito antes de resolver el problema. En ella se ve que en ningún caso habrá tensión sxx, por lo que esta aproximación ni siquiera puede recoger el empuje lateral que hay en el lado izquierdo de la presa. Además, sxy será en todo caso proporcional a y, con lo que se anulará en la base de la presa. Sabemos que esto no puede ser así en realidad, ya que el equilibrio de fuerzas horizontales requiere unas tensiones tangenciales en la base. En resumen, la aproximación de tensiones es un desastre. Pero debe entenderse que ello no es debido a que hayamos hecho las integrales con poca precisión, etc, sino a que las funciones aproximantes elegidas no son lo bastante complejas o adecuadas. Es usual en todos los métodos numéricos que la variable fundamental (desplazamientos en nuestro caso) se aproxime mejor que las variables que se obtienen derivándola (como las tensiones). En todo caso la distribución de tensiones pedida resulta:
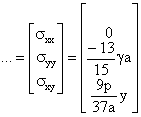
![]()