La evolución de srr debe ser del tipo sen2q. Consideramos por tanto los últimos 4 términos de Airy de la tabla, haciendo n=2:
f = (Ar4 + Br0 + Cr2 + Dr-2) sen2q
srr = (-4Br-2 - 2Cr0 - 6Dr-4) sen2q
srq = (-6Ar2 + 2Br-2 -2Cr0 + 6Dr-4 ) cos2q
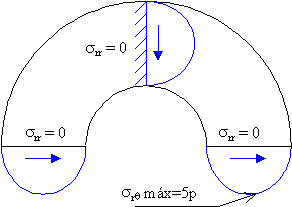
Imponiéndole a esta solución las condiciones de contorno del problema, que son:
en r=re srr = -p sen2q ; srq=0
en r=ri srr = 0 ; srq=0
Obtenemos el siguiente sistema de ecuaciones:
| - 4re-2 B | - 2 C | - 6re-4 D | = - p | |
| - 4ri-2 B | - 2 C | - 6ri-4 D | = 0 | |
| - 6re2 A | + 2re-2 B | - 2 C | + 6re-4 D | = 0 |
| - 6ri2 A | + 2ri-2 B | - 2 C | + 6ri-4 D | = 0 |
Resolviendo para ri=4, re=5, se obtiene:
A=-0.1314 ; B=-179.97 ; C=8.7791 ; D=1170.55
Lo que determina el campo de tensiones pedido. Es notorio que el condicionamiento numérico del sistema de ecuaciones se deteriora notablemente cuando la diferencia de radios es pequeña en comparación con su magnitud. Para el caso estudiado, de radios 4 y 5m, el determinante de la matriz de coeficientes es ya 6 órdenes de magnitud menor que para radios 1 y 2m.
La figura siguiente muestra la distribución de tensiones srq allí donde son mayores: en las bases y en el plano vertical de simetría. Cabe destacar su valor máximo, del orden de 5p en r=4.5m.

![]()