Pensemos en un eje x1 horizontal y en un eje x2 vertical, aunque todavía no precisemos dónde está su origen.
Si se observan las condiciones de contorno, se apreciará que la tensión tangencial, como componente del tensor de tensiones, es de signo distinto en las superficies izquierda y derecha. Por lo tanto tiene que haber una evolución de la tensión s12 con la coordenada x1 (no puede ser constante). Lo menos que puede ser es lineal en x1, lo que nos sugiere una función de Airy que al menos sea del tipo
f = A x12x2
para que al derivar s12 = -f,12 = -2A x1 resulte una función lineal en x1. Además, s12 debe tener el mismo valor y signo opuesto en las caras derecha e izquierda. Si situamos el origen de coordenadas en cualquier punto del plano de simetría (vertical), dichas caras quedan descritas por x1=+b, x1=-b respectivamente (b es el semiancho de la barra).
El término de Airy considerado producirá, además de las tensiones tangenciales, tensiones normales s22 = f,11 = 2A x2, lineales en x2. Si colocamos el origen de coordenadas en la cara inferior, la misma quedará sin tensiones normales, y la cara superior con una cierta tensión, que ha de tener resultante P. Imponiendo las condiciones de contorno:
s12(x1=b) = -2A b = t => A = -t /(2b)
s22(x2=L) = 2A L = - P / (2be) => A = - P / (4beL)
s11(x2=0) = 0
Las dos primeras ecuaciones parecen contradecirse, ya que dan dos valores distintos de A. Lo que ocurre es que en realidad los valores de P y t no pueden ser independientes, ya que deben ser tales que se cumpla el equilibrio vertical de la barra. En efecto, la ecuación de suma de fuerzas verticales igualada a cero implica P = 2tLe, que es exactamente la relación que se obtiene al igualar las dos expresiones de A anteriores. Obsérvese cómo el uso de la función de Airy, al proporcionar tensiones siempre en equilibrio, restablece el equilibrio del sistema, aunque a nosotros "se nos había pasado por alto" hacerlo.
Por tanto no hay contradicción y el término de Airy considerado proporciona las tensiones t en las caras laterales, y la compresión que da como resultante P en la sección superior, dejando sin tensión normal la sección inferior.
Falta la compresión lateral s. No es muy preocupante, ya que sabemos que un término de Airy de la forma Bx22 proporciona tensiones constantes s11=2B. Imponiendo la condición de contorno correspondiente, se obtiene inmediatamente que B=-s/2.
Por tanto la solución encontrada del problema es:
__________________________________
Fución de Airy: f = -(t /2b) x12x2 - (s/2) x22
Tensiones: s11= f,22 = -s
s22 = f,11 = -(t/b) x2
s12 = -f,12 = (t/b) x1
Relación t-P: P = 2eL t
(origen de ejes en el punto medio de la sección inferior)
_____________________________________

_____________________________________
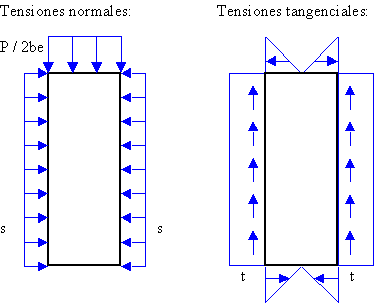
La figura muestra las tensiones de contorno para la solución encontrada, que efectivamente satisfacen las condiciones de contorno del problema. Se observa la existencia de unas tensiones tangenciales de resultante nula en las secciones superior e inferior, que no invalidan la solución ya que se ha dado por aceptable que las condiciones de contorno en esas secciones se satisficieran en forma débil.
Nota: Una forma alternativa de enfocar el problema es tomar el origen de coordenadas en un punto particular a discreción desde el principio, considerar una función de Airy con todos los términos de tercer y segundo grado, y proceder sistemáticamente a calcular sus constantes indeterminadas aplicando las condiciones de contorno. Procediendo así hay que pensar menos, pero se opera más.
![]()