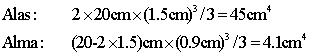
Se trata de un perfil de pared delgada abierto, de modo que usaremos las fórmulas basadas el el "rectángulo estrecho" para estimar la constante de torsión del perfil. A la vista de la geometría del perfil HEB200, podemos calcular sobre la base de 2 rectángulos de 200x15mm2 (las alas), y un rectángulo de (200-2x15)x9mm2 (el alma del perfil). La constante de torsión de cada rectángulo se obtiene con la fórmula be3/3. Así:
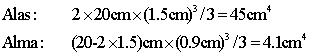
La constante de torsión del perfil es la suma de las de los rectángulos:
J = 45 + 4.1 = 49.1 cm4
NOTA: Este valor tiene una discrepancia apreciable (-21%) respecto del valor que ofrecen las tablas, que es 63.4cm4. La propia norma de estructuras metálicas EA-95 en su apartado 3.A3 propone unas recomendaciones de cálculo al respecto, que podríamos resumir muy someramente en lo siguiente:
Para secciones en forma de L, +, C, z, T, el cálculo de la constante de torsión mediante la aproximación de rectángulos estrechos, tiene buena precisión. Pero en secciones en forma de "doble T" como la de este problema, prevé un error por defecto apreciable, y recomienda multiplicar por 1.3 la constante obtenida con dicha aproximación.
Si tenemos en cuenta esta recomendación, adoptaríamos como valor mas realista de la constante de torsión 49.1x1.3=63.8cm4, que es muy próximo al que figura en tablas.
![]()