La expresión de la submatriz correspondiente al nodo "i" del término de cargas f es, en lo que hace al caso:
![]()
La clave para saber si fi será o no nula es observar si hay soporte común de las funciones que figuran en el integrando. Evidentemente, si no hay soporte común el integrando será cero en todos los puntos, y la integral nula. En nuestro caso, tenemos que observar si en el contorno del sólido (la integral es de contorno) hay soporte común de la función de forma Ni del nodo i con la función X.
Tomemos como ejemplo el nodo 1. En el contorno, su función de forma N1 evoluciona linealmente desde un valor unidad en el nodo 1 hasta cero en el nodo 2. Fuera de ese intervalo su valor es cero. ¡ Nótese que esto es todo lo que necesitamos saber acerca de N1 ! No necesitamos saber su valor en el interior del sólido para realizar una integral de contorno.
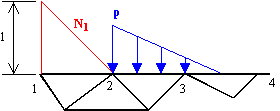
La figura anterior muestra la evolución de la carga y de N1. Como se aprecia, no hay ningún punto del contorno en el que sean distintas de cero las dos a la vez, luego su producto será nulo en cualquier punto considerado. Por tanto es f1 = 0, en lo que a la aportación de la carga considerada se refiere.
Razonando de esta manera, nos damos cuenta de que las aportaciones no nulas se darán en los términos f2, f3, y f4. Puede resultar llamativo que haya aportación a f4 siendo nula X en el nodo 4, pero lo cierto es que tanto f4 como X son distintas de cero en la primera mitad del recorrido desde el nodo 3 al 4. Habiendo ese soporte común, la integral no será cero.
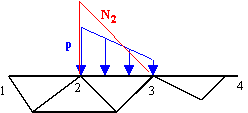
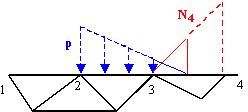
Para calcular f2, tenemos que integrar entre los nodos 2 y 3 el producto de f2 (en rojo en la figura siguiente) por X (en azul). Para hacer la integral se toma cualquier origen de una coordenada x que usaremos para describir el contorno. Seguidamente se expresan las funciones respecto de esa coordenada, y se integra entre los límites de x que correspondan a los nodos 2 y 3. Los detalles son sencillos y bien conocidos. El resultado es:
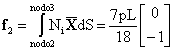
Para calcular f3, tenemos que integrar entre los nodos 2 y 3, y en la primera mitad del tramo entre los nodos 3 y 4. La forma de las funcione se muestra en la figura siguiente. Esta vez, N3 tiene distinta expresión analítica antes de 3 y después, lo que no impide que la consideremos como una sola función, aunque por ejemplo para integrar nos sea conveniente considerarla por tramos. Realizando la integral en dos tramos empleando cualquier origen de x resulta:
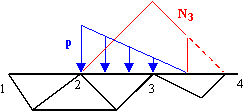
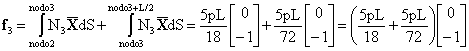
Finalmente, para calcular f4 hay que integrar en un tramo de longitud L/2 desde el nodo 3 hacia el 4. La forma de las funciones se muestra en la figura siguiente. El resultado de la integral es:
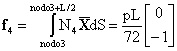
![]()