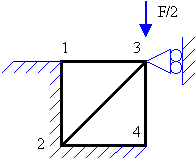
a) El problema es simétrico respecto del plano medio vertical. Teniendo esto en cuenta, podemos simplificar el problema del modo que indica la figura.

b) La estructura del sistema de ecuaciones correspondiente a la simplificación anterior, será:
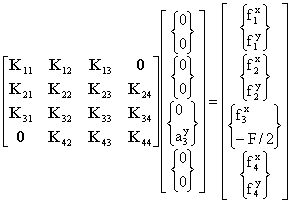
Se han indicado tanto los términos nulos como los que tienen un valor conocido distinto de cero.
c) Se trata de calcular a3y, que por otra parte es la única incógnita de desplazamientos del problema. Observando la estructura del sistema de ecuaciones, nos percatamos de que solo será necesario el tercer par de ecuaciones (la fila que contiene a las submatrices K31, K32, etc.). En este par de ecuaciones tendremos dos incógnitas: a3y, f3x, por lo que esperamos un sistema resoluble. Incluso en esta tercera fila, todas las submatrices de rigidez se multiplicarán por cero, salvo K33. Por tanto solamente es necesario calcular esta submatriz de rigidez. El sistema de ecuaciones para el cálculo de desplazamientos se reduce a:
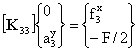
![]()