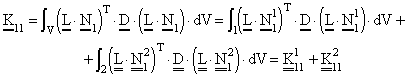
La matriz K que resulta de aplicar el MEF es una matriz cuadrada, formada por submatrices Kij de dimensiones (2x2) en problemas bidimensionales. Cada submatriz se expresa como:
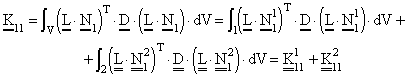
Cada integral como la anterior debe evaluarse allí donde el integrando no sea nulo, es decir, en el soporte común de las funciones Ni y Nj. Por ejemplo, K11 debe evaluarse en todo el soporte de N1, que está formado por los elementos 1 y 2. Por tanto:
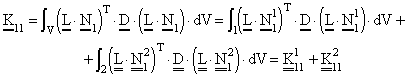
Análogamente, K12 debe evaluarse en el soporte común de las funciones N1 y N2, que en este caso es solamente es el elemento 2, por lo que sólo habrá una aportación a esa sumbatriz de K. Como tenemos 5 nodos, habrá 5x5 submatrices de 2x2. En términos escalares, K será de 10x10.
En la figura se dibuja con un color distinto cada elemento, y en la matriz K global (representada por sus 5x5 submatrices) se dibuja un trazo del mismo color en cada submatriz en la que haya una aportación del elemento correspondiente. Las submatrices sin ningún trazo serían nulas.
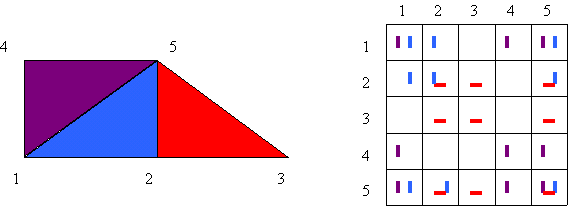
Como es sabido, la matriz K es simétrica, por lo que muchas veces obviamos indicar los valores de los elementos por debajo de la diagonal principal, aunque en este caso sí se hayan indicado.
![]()