Comenzaremos por buscar la solución del problema de la cuña.
La presencia de una carga puntual nos sugiere que las tensiones tendrán que tender a infinito al acercarnos al vértice por el interior del sólido, por lo que buscamos en la tabla tensiones del tipo r-n. Por otra parte, las caras q =+a, q=-a de la cuña están descargadas, es decir que en ellas debe ser srq=sqq=0. Antes de plantear posibilidades más complicadas, reparamos en que hay dos términos de función de Airy que tienen srq=sqq idénticamente nulos en todos los puntos, y cuya componente srr es del tipo 1/r. Estos términos de Airy son:
rq sen q => srr = 2r-1cos q rq cos q => srr = 2r-1sen q
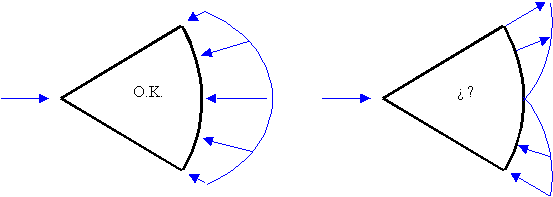
Considerando una porción de cuña limitada por una superficie r = cte, estas tensiones srr serían respectivamente de la forma que se indica a continuación:

Resulta evidente que la figura izquierda puede estar en equilibrio, ya que las tensiones tienen resultante hacia la izquierda, que se opondrá a la fuerza puntual, no hay resultante en sentido vertical, y el momento de todas las fuerzas actúantes es nulo respecto del vértice. La figura derecha en cambio no puede estar en equilibrio, ya que hay una componente vertical de las tensiones que hace incumplir el equilibrio en dirección vertical.
Por tanto, la función f = rq sen q, resuelve el problema de la cuña, lo que responde al primer requerimiento del enunciado.
En cuanto al segundo requerimiento, hay que pensar que el hecho de que hagamos a=p para que la cuña cubra todo el espacio, no garantiza que reproduzcamos un medio continuo. Solamente estaríamos reproduciendo un medio continuo si el campo de desplazamientos fuese univaluado. Puede observarse que esto no sucede sin más que consultar las tablas de desplazamientos, ya que nuestro término de Airy tiene términos no armónicos en q (del tipo qsenq en ur y qcosq en uq) que producen valores múltiples del desplazamiento al considerar el mismo punto como (r,q), (r,q+2p), (r,q-2p), etc.
![]()