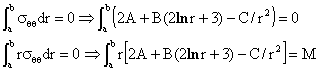
El problema tiene plano de simetría vertical. Si aislamos una mitad, en la sección de corte tendrá que haber resultante nula y momento M, para que el medio sólido esté en equilibrio. Nuevamente el medio sólido tiene un plano de simetría, y nuevamente al aislar su mitad debe haber resultante nula y momento M, y así sucesivamente. Este razonamiento de simetrías sucesivas indica que el problema es axisimétrico, del tipo particular en los que srq = 0. Por tanto probamos una función de Airy que tenga todas las componentes de los problemas planos axisimétricos (k=0 en las tablas), salvo la única que produce srq:
f = A r2 + Br2 lnr + Clnr
Nótese que en este caso, al no existir continuidad del sólido en la coordenada q, es aceptable la presencia del segundo sumando, aunque implique multivaluación de desplazamientos. Las tensiones que derivan de esa función se obtienen de las tablas, y son:
srr = 2A + B(2lnr + 1) + C/r2 ; srq = 0 ; sqq = 2A - B(2lnr + 3) - C/r2
Las constantes se calculan imponiendo las condiciones de contorno. En este caso, las tensiones normales deben ser nulas en r=a y en r=b, y debe haber resultante nula y momento M en las secciones extremas:
2A + B(2lna + 1) + C/a2 = 0 (1ª)
2A + B(2lnb + 1) + C/b2 = 0 (2ª)
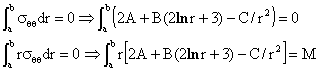
La última ecuación corresponde al momento de las tensiones en las sección respecto del origen de coordenadas. Por tratarse de un sistema de vectores de resultante nula, es indiferente respecto de qué punto se tomen momentos. realizando las integrales obtenemos respectivamente:
(2A+B)(b-a) + 2B(blnb - alna) + C(1/b - 1/a) = 0 (3ª)
A (b2-a2) + B (b2lnb - a2lna) + C ln(b/a) = M (4ª)
Parece que el conjunto de ecuaciones anterior (marcadas 1ª, 2ª, 3ª y 4ª) no podrá resolverse, ya que hay cuatro ecuaciones y sólo tres incógnitas. Sin embargo se aprecia que no son ecuaciones independientes, ya que por ejemplo (3ª) = -a(1ª) +b(2ª). Por tanto el sistema es resoluble. Prescindiendo de cualquiera de las ecuaciones 1ª, 2ª o 3ª, y operando rutinariamente se llega a:
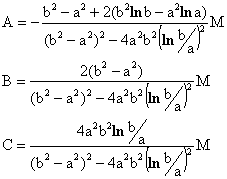
Que determinan el campo de tensiones. Por ejemplo, puede comprobarse que cuanto menor canto tiene la viga (b/a poco mayor que uno) las tensiones srr son tanto menores en comparación con sqq, y que sqq tiene una evolución de apariencia tanto mas lineal en la sección.
![]()