
Comenzaremos por sustituir las reacciones en los apoyos, de valor pa, por distribuciones de tensiones estáticamente equivalentes en las secciones extremas. Tendrán que ser tensiones tangenciales, para que tengan dirección vertical. Como sabemos, su distribución tendrá que ser al menos parabólica para que las esquinas tengan tensión tangencial nula (en las caras superior e inferior no estamos autorizados a modificar las condiciones de contorno). Elegimos por tanto una evolución de tensión tangencial que se anule en x2 = +- b, como se indica.

El polinomio de Airy más sencillo que puede adaptarse a los requisitos en x1 = +- a, es de segundo grado en x2. Como s12 = -f,12 , hemos de considerar una función de Airy al menos cúbica en x2 y al menos lineal en x1. Por otra parte, las tensiones s22 deben variar al menos linealmente con x2, para poder tomar el valor -p en x2=b, y cero en x2=-b, y ser constantes al variar x1. Como s22=f,11 tenemos que considerar una función de Airy al menos lineal en x2 y cuadrática en x1. Por tanto, los mayores órdenes necesarios para reproducir las condiciones de contorno son cuadrático en x1 y cúbico en x2.
Las observaciones anteriores nos ofrecen una orientación acerca del tipo de función f que necesitamos, pero no debe esperarse que incluyendo solamente en f los términos que reproducen las condiciones de contorno se obtenga la solución del problema: debemos plantear una f lo bastante general como para que además podamos ajustar la condición de biarmonicidad. El como dotar a f de generalidad suficiente pero sin llegar a complicar innecesariamente el problema no es una cuestión evidente. En general es preferible incluir términos innecesarios (y encontrar que su coeficiente es cero) a no incluir términos que hubiesen sido necesarios (y tras un tedioso proceso no obtener más conclusión que la función propuesta no resuelve el problema). Teniendo en cuenta lo anterior, y puesto que los mayores órdenes necesarios son cuadrático en x1 y cúbico en x2, podríamos considerar un polinomio completo de grado 3+2=5. Un polinomio completo en x1,x2 , de grado 5 tiene, tras descartar los términos lineales y constante, 18 coeficientes que debemos ajustar.
Podemos simplificar un poco la tarea haciendo intervenir la simetría en tensiones del problema respecto del plano x1=0. En virtud de dicha simetría debe cumplirse:
s11(x1,x2)=s11(-x1,x2) ; s22(x1,x2)=s22(-x1,x2) ; s12(x1,x2)=-s12(-x1,x2)
Las condiciones anteriores se satisfacen si la función f es par en x1. Por tanto limitamos f a la forma:
f(x1,x2) = f1(x2) + x12 f2(x2) + x14 f3(x2) + . . .
Donde fi(x2) son polinomios en x2. Nuestra propuesta de función de Airy será pues un polinomio de grado 5 par en x1. Como las condiciones de contorno sugieren que será suficiente una variación cuadrática en x1, adoptaremos además esta limitación. Cuando estés resolviendo un problema por ti mismo, debes considerar esto último como un riesgo innecesario, ya que no supondría gran complicación incluir los términos x14, x14x2. Proponemos en definitiva el siguiente polinomio como función de Airy:
f(x1,x2) = x12 (C1x23 + C2x22 + C3x2 + C4 ) + C5x25 + C6x24 + C7x23 + C8x22
Intentaremos imponer a este polinomio la condición de biarmonicidad y las condiciones de contorno. El conjunto de condiciones es:
| s12=0 en x2 = +- b |
|
| s22=0 en x2 = - b |
|
| s22=-p en x2 = + b |
|
|
|
|
Las condiciones dadas en forma integral corresponden a la expresión en forma débil de las condiciones de contorno en los extremos x1=+- a de la barra. Las condiciones en forma fuerte (las que figuran a la izquierda) corresponden a los grandes contornos x2=+- b. La condición de biarmonicidad debe imponerse en todo el dominio. Podemos imponer las condiciones en el orden que deseemos, si bien suele resultar operativamente más cómodo comenzar por las condiciones dadas en forma fuerte, y de ellas por las homogéneas (valores dados iguales a cero). Operando así obtenemos:
s12 = 0 = -f,12 en x2 =+-b => 2x1 (3C1b2 +- 2C2b + C3 ) = 0 => C2 = 0 ; C3 = -3b2C1
s22 = 0 = f,11 en x2 =-b => 2 (-C1b3 - C3b + C4 ) = 0 => C4 = -2b3C1
f,1111 + 2f,1122 + f,2222 = 0 = 4 (6C1x2 + 2C2) + 120C5x2 + 24C6 => C5 = -C1/5 ; C6 = 0
s22 = -p = f,11 en x2 =+b => 2 (C1b3 + C3b + C4 ) = -p => C1 = p/(8b3)
Calculado C1 sabemos también C3, C4 y C5. Resumimos lo obtenido hasta aquí:
C1=p/(8b3) ; C2=0 ; C3=-3p/(8b) ; C4 = -p/4 ; C5 = -p/(40b3) ; C6 = 0
Quedan por ajustar las constantes C7 y C8. Pasemos a imponer las condiciones de contorno en forma débil, comenzando por las homogéneas:
![]()
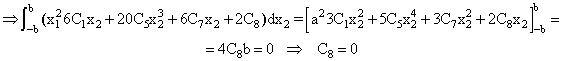
![]()
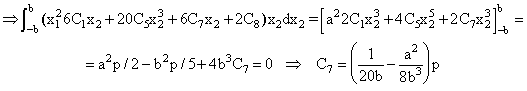
Con esto tenemos calculadas todas las constantes, pero aún nos queda alguna condición por imponer. Si la misma no se satisficiera para los valores de las Ci ya calculados, concluiríamos que la función f propuesta no resuelve el problema, y pasaríamos a proponer otra más general. Comprobamos que, afortunadamente, sí se satisface:
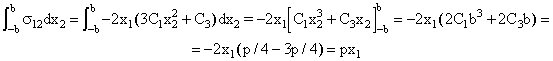
Que efectivamente vale +pa en x1=a, y -pa en x1=-a. La función propuesta satisface todos los requerimientos del problema, y por tanto es una solución del mismo. El estado de tensiones solución es el que deriva de la f calculada:
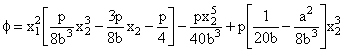
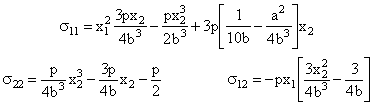
![]()