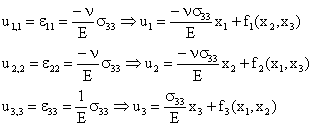
Como se aprecia, este problema se diferencia del anterior en que solamente los movimientos normales están impedidos en la cara inferior del cubo, siendo posible el movimiento de los puntos de dicha cara sin salirse de su plano.
Siendo las tensiones el dato que nos ofrecen, las comprobaciones se reducirán al equilibrio interno y a las condiciones de contorno, tanto en tensiones como en desplazamientos.
Comprobaciones relativas a las tensiones.
El campo propuesto tiene componentes de tensión constantes, por tanto sus derivadas serán nulas, y la ecuación de equilibrio en el dominio sij,j + Xi = 0, se satisfará idénticamente en ausencia de fuerzas de volumen, lo que es el caso. La ecuación de equilibrio en el contorno sij nj = Xi , nos permite comprobar si se satisfacen las condiciones de contorno en tensiones. En este caso es evidente que esas tensiones implican una compresión de valor p en la cara superior, y tensiones nulas en las 4 caras laterales. En la cara inferior no hay tensiones tangenciales, lo que efectivamente concuerda con el enunciado. Nótese que no procede realizar ninguna comprobación acerca de las tensiones normales en la cara inferior, ya que en esa dirección están prescritos los desplazamientos.
Comprobaciones relativas a los desplazamientos.
En primer lugar, debemos cerciorarnos de que sea posible la existencia de un campo de desplazamientos asociado a las tensiones propuestas. Para ello usamos las ecuaciones de Michell y Beltrami, que tienen la forma de sumas de derivadas segundas de las tensiones, igualadas a cero. Como el campo de tensiones es constante, es seguro que se cumplirán estas ecuaciones. Sólo nos queda pues comprobar que el campo de desplazamientos cumple las condiciones de contorno en desplazamientos del enunciado. Para ello calculamos el campo de desplazamientos:
Usando la ley de comportamiento, expresamos las componentes diagonales del tensor de deformaciones en función de las del de tensiones, y realizamos una primera integración:
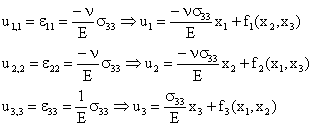
Donde f1, f2, f3, son funciones arbitrarias de las variables indicadas, que pueden tener también un término constante. Si apreciamos que el enunciado impone u3=0 en x3 =0, podemos ya decir que f3(x1, x2 ) = 0.
Incorporamos esta conclusión, y hacemos uso de las componentes transversales de deformación, que serán nulas por serlo las correspondientes componentes de tensión:
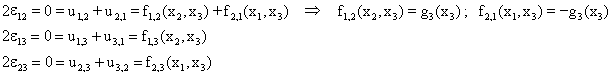
En la primera de las ecuaciones anteriores se ha razonado que para que la suma de dos funciones, una dependiente de (x2,x3) y otra de (x1,x3), sea nula en todo un rango de valores, en realidad las funciones sólo pueden depender de x3. Se ha llamado g3(x3) a una de ellas, y -g3(x3) a la otra, ya que deben sumar cero. Con esto, podemos integrar para expresar f1 y f2 en función de g3 y de unas nuevas funciones indeterminadas de x3. Adicionalmente, las dos últimas ecuaciones indican que f1 y f2 no dependerán en realidad de x3:
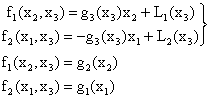
Las ecuaciones que abarca la llave proceden de la primera del conjunto anterior, y las otras dos, de la 2ª y 3ª del conjunto anterior. Identificando la primera y tercera de este conjunto de ecuaciones, solamente se aprecia una posibilidad:
g3(x3) = A ; L1(x3) = B ; g2(x2) = Ax2 + B
Análogamente, la identificación de las segunda y cuarta solo deja una posibilidad:
g3(x3) = A ; L2(x3) = C ; g1(x1) = -Ax1 + C
Por lo tanto:
f1(x2, x3) = Ax2 + B ; f2(x1, x3) = -Ax1 + C
Con lo que el campo de desplazamientos queda:
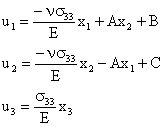
En donde se entiende que s33 tiene el valor dado por el enunciado: s33 = -p.
Nota: Se apreciará que en la solución de desplazamientos han quedado tres constantes por determinar. Tres son también los grados de libertad que un sólido rígido tiene al moverse en un plano. En efecto, estas constantes A, B, C, se corresponden con la posibilidad de movimiento de sólido rígido en el plano 1-2. Si situásemos el origen de coordenadas en algún punto concreto (obsérvese que no lo hemos hecho), y el enunciado nos diese algunas condiciones de contorno en desplazamientos, podríamos determinar estas constantes.
![]()