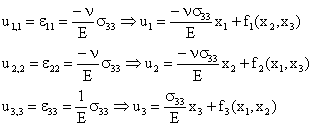
En general, una comprobación de una solución propuesta requiere demostrar que dicha solución satisface las ecuaciones básicas del modelo elástico (equilibrio, compatibilidad y comportamiento), y las condiciones de contorno en desplazamientos y en tensiones.
En este caso particular, solamente nos dan las tensiones. Obtendremos las deformaciones y desplazamientos a partir de esas deformaciones, usando la ley de comportamiento y haciendo una integración de las ecuaciones de compatibilidad, respectivamente. Las comprobaciones propiamente dichas se reducirán al equilibrio interno y a las condiciones de contorno, en este caso.
Comprobaciones relativas a las tensiones.
El campo propuesto tiene componentes de tensión constantes, por tanto sus derivadas serán nulas, y la ecuación de equilibrio en el dominio sij,j + Xi = 0, se satisfará idénticamente en ausencia de fuerzas de volumen, lo que es el caso. La ecuación de equilibrio en el contorno sij nj = Xi , nos permite comprobar si se satisfacen las condiciones de contorno en tensiones. En este caso es evidente, incluso sin necesidad de usar esa ecuación explícitamente, que el campo de tensiones propuesto implica una compresión de valor p en la cara superior, y tensiones nulas en las 4 caras laterales. Nótese que no procede comprobar tensiones en la cara inferior, ya que en ella no hay condiciones de contorno en tensiones.
Comprobaciones relativas a los desplazamientos.
En primer lugar, debemos cerciorarnos de que sea posible la existencia de un campo de desplazamientos asociado a las tensiones propuestas. Para ello usamos las ecuaciones de Michell y Beltrami, que básicamente son el equivalente a las ecuaciones de integrabilidad, pero en función de las tensiones y asumiendo que se satisfacen las ecuaciones de equilibrio, lo que ya hemos comprobado. En ausencia de fuerzas de volumen, las ecuaciones de Michell y Beltrami, tienen la forma de sumas de derivadas segundas de las tensiones, igualadas a cero. Como el campo de tensiones es constante, es seguro que sus derivadas segundas serán nulas, y por lo tanto se cumplirán estas ecuaciones. Sólo nos queda pues comprobar que el campo de desplazamientos cumple las condiciones de contorno en desplazamientos del enunciado. Para ello tenemos que calcular el campo de desplazamientos, lo que se hace seguidamente.
Usando la ley de comportamiento, expresamos las componentes diagonales del tensor de deformaciones en función de las del de tensiones, y realizamos una primera integración:
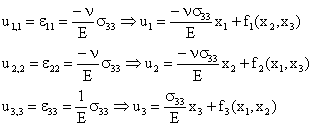
Donde f1, f2, f3, son funciones arbitrarias de las variables indicadas, que pueden tener también un término constante. Ahora nos dispondríamos a expresar las deformaciones transversales -conocidas-, en función de los desplazamientos para continuar el proceso de integración. Pero si observamos lo que ya hemos obtenido, nos podemos ahorrar el trabajo: vemos que u1 no puede anularse en la cara base del sólido, ya que tiene una componente proporcional a x1 que no puede cancelarse con ningún otro término (cualquiera que sea la forma de f1) para todo el rango de valores de x1 que describe dicha cara base. Lo mismo puede decirse de u2 respecto de x2.
Por lo tanto, las condiciones de contorno en desplazamientos no pueden satisfacerse con las tensiones propuestas en el enunciado, así que dichas tensiones NO son la solución de nuestro problema.
Nota: De la tercera ecuación no cabe inducir ninguna incompatibilidad, ya que f3 podría ser nula, y de esa manera se satisfaría la condición u3=0 en x3=0. Por supuesto no es necesario que haya incompatibilidades en todas las ecuaciones para descartar una solución. Es suficiente con que las haya en alguna de ellas.
![]()