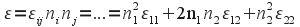
El procedimiento a seguir será plantear el alargamiento unitario de cada filamento en función de las componentes (desconocidas) del tensor de deformaciones. Esto proporciona tantas ecuaciones como filamentos, -tres-, siendo las incógnitas las componentes del tensor, -también tres-. Por tanto el sistema de ecuaciones será en principio resoluble.
Puesto que el cálculo ha de repetirse para tres direcciones, conviene plantear primero la expresión del alargamiento e en una dirección genérica n:
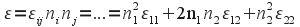
Particularizando esta ecuación en las tres direcciones de los filamentos, nA, nB, nC, que están dadas por:
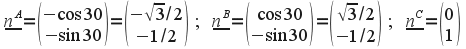
Se obtienen las siguientes ecuaciones:

La tercera ecuación es ya parte del resultado buscado. Al coincidir la dirección de C con la del eje 2, era evidente que sus deformaciones debían ser idénticas. Sustituyendo la tercera en las dos primeras y operando, se despejan sin dificultad las otras dos incógnitas. El resultado es:
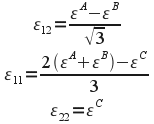
![]()