
Para calcular el incremento de longitud del filamento, definamos un vector t, tangente al mismo en cada punto. Como se aprecia en la figura, sus componentes serán (-sen q, cos q).

El incremento unitario de longitud viene dado por eij ti tj . El incremento de longitud total será la integral de ello a lo largo de la longitud del filamento:
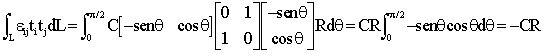
Por tanto se trata de un acortamiento, indicado por el signo menos del resultado.
El incremento unitario de superficie en un punto de la placa, viene dado por e11+e22 . El incremento de superficie total de una región, será su integral extendida a la región considerada. En nuestro caso, e11+e22 = 0, por lo tanto su integral también lo será. La conclusión es que el cuarto de círculo, al igual que cualquier otra porción de la placa, no sufre variación de área.
![]()