![]()
Cálculos con ecuaciones en derivadas.
CONCEPTO DE DERIVADA
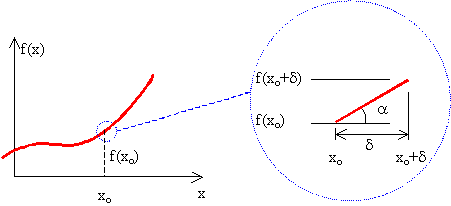
Derivada en un punto de funciones de una variable (derivada total usual). Como es sabido, una derivada de una función f(x) en un punto xo se obtiene comparando el valor de la función en ese punto y en otro muy próximo. Bajo ciertas condiciones, que f(x) debe cumplir en en entorno de xo, el cociente entre la diferencia de valores de la función y la diferencia de valores de la variable tiende a un límite, que llamamos derivada. Junto a la figura se indican varias notaciones usuales para la derivada calculada. El valor de la derivada en el punto coincide con la pendiente (tga) de la recta tangente a la función en ese punto, en una representación como la de la figura.
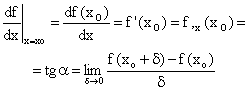
Expresión analítica de la función derivada. Si se calcula la derivada de una función en todo un rango de valores de la variable, obtenemos una nueva función definida en ese rango, que llamamos función derivada. Esta última puede a su vez derivarse, y obtenemos la derivada segunda de la función original. Operando similarmente con la derivada segunda se obtiene la derivada tercera, etc. Seguidamente se indican algunas de las notaciones para las funciones derivadas segundas de funciones de una variable:
![]()
Las derivadas de todas las funciones usuales tienen expresión analítica conocida, que pueden buscarse en tablas de derivadas, aunque debemos saber de memoria las más comunes, como f(x)=xn =>f'(x)=nxn-1 , etc. Por supuesto, en la práctica no calculamos un límite cada vez que queremos saber el valor de una derivada (ya sea primera o de orden superior) en un punto concreto. En su lugar solemos calcular la función derivada y particularizamos las variables en las coordenadas del punto.
CONCEPTO DE DERIVADA PARCIAL
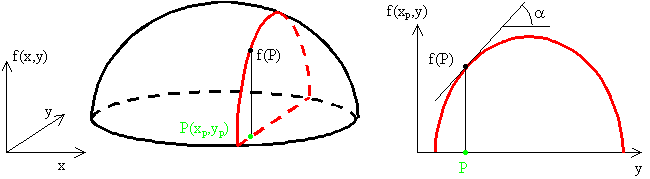
Derivada en un punto de funciones de varias variables (derivada parcial). Cuando la función depende de varias variables, la derivada parcial en un punto respecto de una de ellas se calcula manteniendo constante el valor de las demás, y procediendo como si la única variable fuese la de derivación. En la figura se representa una función de dos variables, x e y. Como se aprecia, su derivada respecto de y en el punto P se calcula como en el caso de una variable, sin mas que considerar el corte de la función por el plano x=xp.
A continuación se indican algunas de las notaciones y propiedades de la derivada parcial, en relación con el ejemplo de la figura anterior:
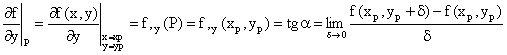
Expresión analítica de la función derivada en el caso de varias variables. Si se calcula la derivada parcial (digamos respecto de y) de una función en toda una región de valores de las variables (x,y), obtenemos una nueva función definida en esa región, que llamamos función derivada parcial (respecto de y), y cuya expresión analítica es igual de fácil de encontrar que en el caso de una variable. Podemos a su vez calcular la derivada respecto de y de esta nueva función (obtenemos la derivada segunda respecto de y dos veces), o respecto de x (obtenemos la derivada segunda respecto de "y" y respecto de "x"). Seguidamente se indican algunas de las notaciones para las funciones derivadas segundas de funciones de dos variables:
![]()
Bajo ciertas condiciones de regularidad, que las funciones relacionadas con fenómenos físicos casi siempre satisfacen, el orden de derivación en una derivada de orden superior no afecta al resultado (teorema de Schwarz). Por ejemplo, en el caso anterior la propiedad aludida implica que f,xy=f,yx.
CÁLCULOS CON ECUACIONES EN DERIVADAS
En la asignatura se necesitará manejar algunos sistemas de ecuaciones diferenciales, y calcular sus integrales. Los procesos de integración que realizaremos requieren solamente algunas ideas sencillas, que dimanan directamente del concepto de derivada parcial. No se necesitará aplicar los métodos especializados de integración de ecuaciones diferenciales que suelen estudiarse en las asignaturas que tratan específicamente el tema. En este apartado se ilustran las ideas sencillas aludidas.
En primer lugar, recordemos que el conocer alguna derivada de la función f(x), nos permite obtener cierta información acerca de la propia función f. A continuación se enumeran sin ánimo de exhaustividad algunos ejemplos.
|
Si en todo un rango de valores de las variables, f satisface: |
Entonces, f tendrá la forma: | Observaciones: |
| f,x(x)=0 | f(x)=C | C = constante arbitraria |
| f,x(x,y)=0 | f(x,y)=C(y) | C(y) = función arbitraria de y, que puede incluir una constante |
| f,xy(x,y)=0 | f(x,y)= C(x)+D(y) | C(x), D(y), funciones arbitrarias, que pueden incluir una constante |
| f,xx(x,y)=0 | f(x,y)=xC(y)+D(y) | C(y), D(y), funciones arbitrarias, que pueden incluir una constante |
| f,x(x)=xn | f(x)=xn+1/(n+1) + C | C = constante arbitraria |
| f,x(x,y)=xn | f(x)=xn+1/(n+1) + C(y) | C(y) = función arbitraria de y, que puede incluir una constante |
| f,xy(x,y)=xn | f(x,y)= yxn+1/(n+1)+C(x)+D(y) | C(x), D(y), funciones arbitrarias, que pueden incluir una constante |
En segundo lugar, adelantemos que el modelo matemático de la Teoría de la Elasticidad involucra solamente ecuaciones lineales. En particular, serán sistemas de ecuaciones diferenciales de primer orden lineales en derivadas parciales de coeficientes constantes.
La nomenclatura que se está usando para las ecuaciones diferenciales es la siguiente (como excepción, no es preocupante que no te sean familiares algunos tipos):
Ecuación diferencial: la que contiene derivadas de la función incógnita respecto de las variables. Puede aparecer también la función sin derivar, y términos que contengan a las variables.
Ordinaria: Ecuación diferencial en la que sólo hay una variable independiente.
En derivadas parciales: Ecuación diferencial con varias variables independientes.
Orden de una ecuación diferencial: el mayor orden de derivación que aparece en la misma.
Lineal: Ecuación diferencial en la que las derivadas no aparecen multiplicadas entre sí, ni elevadas a potencias distintas de uno.
De coeficientes constantes: Ecuación diferencial en la que los factores que multiplican a las derivadas son constantes.
Sistema de ecuaciones diferenciales: un conjunto de ecuaciones diferenciales que deben satisfacerse a la vez. Habrá presentes varias funciones incógnita. Los sistemas de ecuaciones diferenciales tendrán varias funciones incógnita y varias variables.
Integrales de una ecuación diferencial: una o varias ecuaciones que contienen a las funciones (sin derivar) y a las variables, y que satisfacen idénticamente la ecuación diferencial. Integrar una ecuación diferencial es hallar todas sus integrales posibles. Llamamos solución a una integral en la que la función incógnita está despejada en función de las variables. Solución general es la que contiene como casos particulares a todas las soluciones posibles. Las integrales y soluciones suelen contener constantes o funciones arbitrarias (que pueden elegirse arbitrariamente).
Condiciones de contorno: valores concretos que debe tener la función incógnita o sus derivadas en determinados puntos o regiones, que suelen estar en el contorno (del sólido en nuestro caso). Habitualmente permiten concretar las constantes o funciones arbitrarias.
Solución particular: una solución que no contiene constantes ni funciones arbitrarias. Corresponde a unas condiciones de contorno particulares.
En tercer lugar, recordemos un detalle que necesitaremos, relativo a la estructura de la solución de las ecuaciones diferenciales lineales. Como se ha dicho, las que aparecen en la asignatura son de este tipo. Para centrar ideas, consideremos por ejemplo la siguiente ecuación lineal:
a.f(x) + b.f'(x) + c.f''(x) = F(x)
En donde f(x) es la función incógnita, las a, b, c, pueden ser constantes o funciones de x, y F(x) es una cierta expresión en x.
Nomenclatura utilizada: Si F(x)=0, la ecuación se llama homogénea, y no homogénea o "completa" en caso contrario. Un conjunto de tantas soluciones independientes de la ecuación homogénea como orden tenga la ecuación (dos en este caso), se llama sistema fundamental de soluciones de la ecuación homogénea.
Si f1(x), f2(x), constituyen un sistema fundamental de soluciones de la ecuación homogénea (para F(x)=0), entonces la combinación lineal C1.f1(x)+C2.f2(x), que llamaremos fh(x), es solución general de la ecuación homogénea (C1 y C2 son constantes arbitrarias). El hecho importante que necesitaremos y que queremos recordar es el siguiente:
La solución general de una ecuación diferencial lineal completa (no homogénea), se obtiene sumando la solución general de la homogénea y una solución particular cualquiera de la completa.
En nuestro caso, si es fp(x) una solución particular, la solución general de la ecuación completa vendrá dada por f(x)=fh(x)+fp(x). Nótese que la "generalidad" de esta solución general de la completa está aportada por la solución general de la homogénea fh(x), a través de sus constantes indeterminadas.
En cuarto lugar, finalicemos recordando que las ecuaciones lineales, ya sean diferenciales o no, permiten aplicar el principio de superposición de efectos. En la asignatura haremos uso constantemente de esta propiedad. Es de aplicación tanto a los términos no homogéneos de las ecuaciones (F(x) en el ejemplo anterior), como a las condiciones de contorno.
DESARROLLOS EN SERIE
Desarrollo en serie de potencias (Serie de Taylor).
Bajo ciertas condiciones de regularidad, que las funciones relacionadas con fenómenos físicos habitualmente satisfacen, el valor de una función f(x) en un punto x está relacionado con el valor f(x+d) en otro punto x+d mediante la expresión:
![]()
Donde el "Residuo" es del orden de dn+1. Para funciones de varias variables, f(x,y,...z), se consideran unos incrementos que pueden ser distintos para cada variable, dx, dy, ... dz, y la expresión a aplicar es:
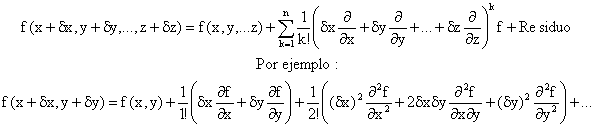
Desarrollo en serie armónica (Serie de Fourier).
En la asignatura se hará uso eventual (sólo en dos ocasiones concretas) de desarrollos en serie de Fourier, y se aplicará a una sola de las variables independientes, con lo que el desarrollo en serie permanece en el ámbito de las funciones de una variable. Es suficiente con conocer la "receta" más elemental de las series de Fourier, que se recuerda seguidamente.
Bajo ciertas condiciones de regularidad, que las funciones relacionadas con fenómenos físicos habitualmente satisfacen, el valor de una función f(x) en el intervalo 0 < x < 2p puede aproximarse con tanta precisión como se desee mediante un número suficiente de términos (n lo bastante grande) de la siguiente serie:
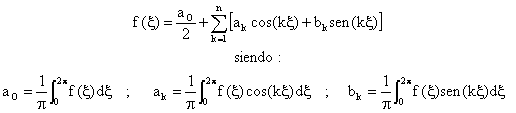
Usualmente la variable independiente será x, y desearemos aproximar f(x) en un intervalo diferente de (0,2p), por ejemplo a<x<b. Para ello sólo hay que aplicar el cambio lineal de variable x = a + x(b-a) / 2p. El cambio de variable en las integrales requiere las precauciones conocidas (multiplicar por el Jacobiano de la transformación, etc).
DIFERENCIAL DE UNA FUNCIÓN
El incremento de una función f, según su definición habitual, es la diferencia de su valor en dos puntos distintos, separados una cierta distancia. Interesa aquí el caso en que los dos puntos estén separados una distancia diferencial. Nos referiremos a este caso en lo sucesivo, y denotaremos Df al incremento de f entre un punto (x, y,..., z) y otro (x+dx, y+dy,..., z+dz) donde dx,..., dz son diferenciales de las variables respectivas.
Aunque el orden de exposición no sea riguroso (el concepto de diferencial es anterior al de desarrollo en serie), en el presente contexto nos permitiremos obtener el valor del incremento a partir del desarrollo en serie de Taylor, para destacar sus similitudes. Considerando que d es diferencial en las expresiones de Taylor para una y dos variables, se obtiene respectivamente:
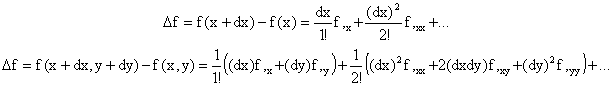
En ambos casos el incremento se obtiene como producto de diferenciales de variables por derivadas de la función, más infinitésimos de orden superior. Llamamos DIFERENCIAL de la función al primer término del desarrollo en serie del incremento. En los casos de una y dos variables anteriores, tenemos:
df(x) = f,x dx
df(x,y) = f,x dx + f,y dy
Para mayor número de variables independientes, la expresión del diferencial se obtiene de forma análoga. Cabe resaltar algunos hechos acerca de los diferenciales:
- El valor del incremento, y del diferencial, dependen de la distancia y posición relativa entre el punto considerado y el próximo de su entorno (que está a distancias dx, dy, ... en las direcciones respectivas).
- El diferencial nos da el valor del incremento, salvo diferenciales de orden superior. Para funciones de una variable puede interpretarse como el incremento que se obtendría siguiendo la recta tangente al punto considerado, en lugar de la curva real que representa a la función.
- Los modelos matemáticos utilizados para describir fenómenos físicos se construyen casi exclusivamente aproximando los incrementos por diferenciales, despreciando así diferenciales de orden superior. Se llaman modelos de primer orden, o teorías de primer orden, a los así construidos.
- Los modelos matemáticos clásicos de la Teoría de la Elasticidad, de la Mecánica de Fluidos, y de la Termodinámica, son ejemplos de modelos de primer orden, entre otros muchos. El que puedan conducir a paradojas aparentes en puntos particulares de primeras derivadas nulas (ya que las de orden superior se desprecian), no merma las enormes ventajas prácticas de estos modelos frente a los de orden superior (son no lineales, y son mas difíciles de manejar).
Un mensaje de tranquilizador: No se necesitará recordar procedimientos intrincados de integración (diferenciales binomias, fracciones racionales, integrandos irracionales, etc): las integrales "difíciles" las realizaremos numéricamente mediante cuadratura, o buscaremos la primitiva en tablas. Se requiere más bien tener claro en qué consiste cada tipo de integral, y saber cómo expresar lo que se necesita calcular en cada ocasión, a través de una integral (definida, indefinida, de línea, de volumen...). Ello requiere haber estudiado cálculo integral antes de acceder a la asignatura.
Seguidamente se indica a modo de sumario lo que se necesitará en algún momento del curso en lo relativo al cálculo integral. No se considera que merezca la pena incluir aquí los desarrollos al respecto:
- Las integrales inmediatas más comunes.
- Procedimiento de integración por partes. Se usará en desarrollos teóricos.
- Derivación bajo el signo integral. Se usará en desarrollos teóricos.
- Cambio de variable en integrales (uso del Jacobiano, etc). Ocasionalmente preciso en problemas.
- Integrales dobles y triples (definidas). Usadas extensamente.
- Integrales de línea y de superficie (definidas). Usadas extensamente.
Aunque no es imprescindible, encontrarás facilidades en comprender algunos procedimientos usados en la asignatura si conoces ya algún procedimiento de integración aproximado, como la cuadratura de Gauss o la de Simpson.
![]()