EXAMEN EXTRAORDINARIO DE SEPTIEMBRE

Elasticidad y Resistencia de Materiales – Parte de Elasticidad

ETSII- 3^er Curso (Plan antiguo) – 11 de septiembre de 2000

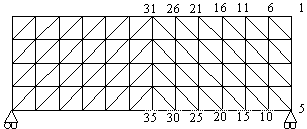
CUESTIÓN PRÁCTICA 1) La figura muestra una discretización plana en Elementos Finitos de una viga corta, cuyas dimensiones son 12Lx4L. La numeración de nodos se realiza por columnas, como se indica parcialmente. Existe una carga uniformemente distribuida en la superficie superior, de valor p kgf/m², dirigida hacia abajo. Opere por unidad de espesor, y asuma coeficiente de Poisson nulo, y Módulo de Young de valor E. Se pide que:

a) Explique la posibilidad de analizar solamente medio sólido (el derecho), e indique la forma que tendrían el término de cargas, f, y el de desplazamientos, a, en dicho análisis. Calcule el valor de los términos que sea posible calcular a priori.

b) Calcule las submatrices K_4-9 y K_4-10 de la matriz de rigidez global. Puede emplear el sistema de ejes que mas cómodo le resulte.

CUESTIÓN PRÁCTICA 2) La media corona circular de la figura está realizada en chapa metálica, y representa uno de los elementos de la estructura de un gran invernadero. La acción del viento sobre otros elementos no mostrados, transmite al contorno exterior de la corona unas tensiones de dirección radial, de valor nulo en el punto superior e inferiores, y máximas (de valor absoluto p) en los puntos de q=45º, como se muestra. Se asumirá que estas tensiones tienen evolución del tipo sen 2q. No hay ninguna acción sobre el contorno r=r_i (interior). Se pide que:

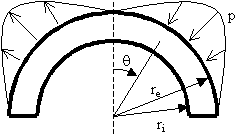
a) Usando las tablas adjuntas de funciones de Airy, plantee una solución de tensiones que satisfaga exactamente las condiciones asumidas en r_i y en r_e . Llegue a plantear explícitamente, y en forma compacta, el sistema de ecuaciones que le permitiría obtener la solución. No es necesario que resuelva el sistema (por favor, no lo haga).

b) Represente aproximadamente (sin más cálculos) como serían las tensiones normales y tangenciales que se obtendrían en los contornos planos inferiores de la media corona.

c) Responda mediante argumentos muy breves, sin cálculos: ¿Existe garantía de que la solución planteada satisfaga las ecuaciones de Michel y Beltrami? ¿Qué implicaciones tiene lo anterior? ¿Cabe esperar que en esta solución haya incrementos de distancia entre dos puntos cualesquiera de las superficies planas inferiores?