EXAMEN FINAL ORDINARIO - ELASTICIDAD Y RESISTENCIA DE MATERIALES

Materia del primer parcial.

ETSII – 3^er curso (plan antiguo)– 5 de julio de 2000

Cuestión 1.- Desarrolle, a su elección, uno de los dos siguientes temas:

a) “Criterio de Von Mises” (Contenido: fundamento en base a la densidad de energía de deformación, obtención de al menos una de sus expresiones, comparación con el criterio de Tresca, y con los ensayos de Lode).

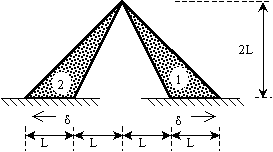
Cuestión 2.- La figura representa dos placas triangulares, 1 y 2 (punteadas), unidas entre sí por su vértice superior. Debido a ciertos efectos de dilatación de la base a la que está unidas, se ha producido un desplazamiento conocido y constante en la base de cada placa de valor d, en los sentidos indicados. Se asumirá Módulo de Young E, Coeficiente de Poisson nulo, y espesor e de las placas. Se realizará una aproximación de Elementos Finitos consistente en un solo elemento triangular para cada placa. Se pide:

a) Indicar las simplificaciones previas que el problema permite. Debe conseguirse una configuración de análisis en la que solo esté presente una de las placas, y en la que solo se mueva uno de los vértices.

b) Calcular las componentes horizontal y vertical de la fuerza que se transmiten entre sí las placas a través del vértice común, según la aproximación en Elementos Finitos planteada. Use las simplificaciones del apartado anterior.

c) Calcular las componentes del vector tensión dadas por dicha aproximación, en el borde superior de cada placa (los inclinados 45º respecto de la horizontal). Utilice obligatoriamente el diagrama de Mohr en este cálculo.

d) Realizar una breve discusión acerca de si la obtención de valores no nulos en el apartado anterior implica necesariamente que se haya cometido error en los cálculos.                                          (1+1+1+0.5=3.5 ptos)

Cuestión 3.- Los pilotes son básicamente barras que se hincan en el terreno, de uso en cimentaciones. La figura muestra una porción de 1m de longitud de un pilote, de sección cuadrada 10cm ´ 10cm. El pilote se ha introducido en una grieta del terreno, quedando aprisionado entre sus caras izquierda y derecha (figura), y no por las delantera ni trasera. Las acciones son: P=8Ton.; Q= 2Ton.; t es la tensión tangencial debida a la fricción con el terreno, y s=60Kgf/cm² es la compresión ejercida por el mismo. Se asumen como aproximaciones que existe estado de Tensión Plana, que s y t son constantes en el metro de pilote analizado, y la posibilidad de imponer condiciones de contorno en forma débil en las caras superior e inferior. Se pide:

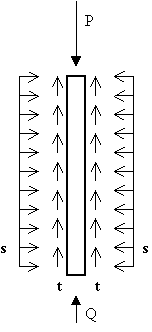
a) Calcular el valor de la tensión tangencial t para que la porción de sólido analizado esté en equilibrio.

b) Indique dónde debe situarse el origen de coordenadas de un sistema de ejes x-y para que, bajo las aproximaciones aceptadas, la función de Airy f=-Ax²y-By² , con A=0.3Kp/cm³, B=30Kp/cm², permita analizar el problema elástico considerado. Comente en particular de qué forma se ha hecho uso de la simplificación de condiciones de contorno en forma débil (incluya una representación de las tensiones que derivan de esa función de Airy para ilustrar el comentario).

c) Basándose en razonamientos sobre diagrama de Mohr, indique cuál es el punto más solicitado de la porción de pilote considerada según el criterio de Tresca. En este apartado, y previa justificación, puede despreciar la/las componentes de tensión que sean poco significativas.                                                    (0.5+1.2+1.3=3 ptos)