ELASTICIDAD Y RESISTENCIA DE MATERIALES - 3er Curso
EXAMEN EXTRAORDINARIO DE ENERO (21 de enero de 2000) - Parte de Elasticidad
Cuestión 1.- La primera figura muestra un sólido que trabaja en condiciones de tensión plana, cuya profundidad (en dirección perpendicular al dibujo) es la unidad. Se pide que:
Especifique de qué manera (mediante qué tipo de distribución de tensiones) deben estar aplicados los momentos en los extremos izquierdo y derecho para que ese problema elástico tenga solución exacta mediante un polinomio de Airy de bajo orden.
Asumiendo que en efecto los momentos están aplicados de esa manera (apartado a), calcule el estado de tensiones empleando un polinomio de Airy de bajo orden.
Comente brevemente las coincidencias o discrepancias entre la solución de tensiones encontrada en el apartado (b) y la que proporciona la Resistencia de Materiales.
Asuma ahora que los momentos están aplicados de alguna otra manera, por ejemplo mediante sendos pares de fuerzas concentradas como indica la segunda figura. Exponga los argumentos que considere oportunos acerca de la validez de la solución encontrada en el apartado (b) para este caso. (Sugerencia: exponga razonadamente si interviene el valor de la relación a/b).
(0.5+1+0.5+1=3 ptos.)

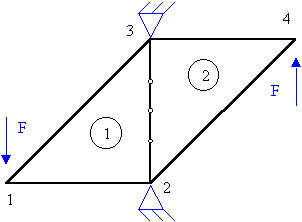
Cuestión 2.- La figura, que asume estado de deformación plana, representa aproximadamente un aspecto del modo de trabajo de determinado elemento de una máquina. Se pide que:
a) Exponga una razón básica que asegura que en este problema no se podrán plantear simplificaciones derivadas de simetría ni antisimetría elástica.
b) Razone si alguna de las componentes de movimiento (u1, u2) del punto A, situado en el centro de áreas del sólido, tendrá valor nulo. Idem. para un punto como B, situado a cierta distancia en la vertical de A. Razone finalmente si existirá alguna relación entre las componentes del movimiento de B y de B', este último situado a la misma distancia de A que B, como se indica. (Sugerencia: aprecie que girando el problema en su plano 180° en torno al punto A, se obtiene una configuración que guarda relaciones evidentes con la inicial).
(0.5+1.5=2ptos.)
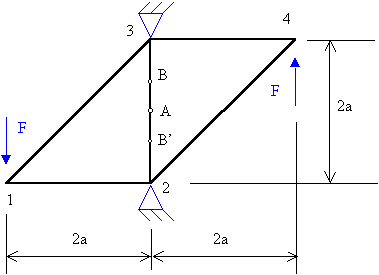
Cuestión 3.- La figura muestra una discretización muy sencilla del problema elástico anterior, en sólo dos elementos finitos triangulares de tres nodos. Asuma módulo de Young E, y coeficiente de Poisson nulo. Sitúe unos ejes coordenados x1, x2, como le parezca conveniente. Se pide que:
a) Calcule la submatriz K11 de la aproximación.
b) Escriba la matriz columna completa de cargas de la aproximación, f. (Deje indicados como incógnitas los términos que no sean conocidos a priori).
c) Argumente acerca de porqué basta con lo calculado en los dos apartados anteriores para poder hallar el desplazamiento del nodo 1.
d) Calcule el desplazamiento del nodo 1.
(1 + 1 + 1+ 1=4ptos.)