EXAMEN EXTRAORDINARIO DE SEPTIEMBRE

INTRODUCCIÓN A LA Elasticidad y Resistencia de Materiales

ETSII- 2º Curso (Plan nuevo) – 15 de septiembre de 2000

CUESTIÓN 1 (teórica).- Considere el siguiente polinomio de cuarto grado (que es completo hasta los términos de grado 2):

Ax⁴ + Bx³y + Cx²y² + Dxy³ + Ey⁴ + Fx³ + Gx²y + Hxy² + Iy³ + Jx² + Kxy + Ly²

Se pide que :

a) Indique si los coeficientes A, B, C, ... etc, deben satisfacer alguna relación para que el polinomio pueda usarse como función de Airy. Exprese en su caso dichas relaciones.

b) Indique qué relaciones tienen que satisfacerse adicionalmente para que el campo de tensiones satisfaga las condiciones de un problema simétrico respecto del eje coordenado “y”.

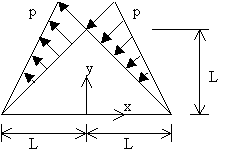
           CUESTIÓN 2.- La figura muestra el problema bidimensional de una placa triangular sometida a las acciones que se indican. Se asumirá espesor unidad, Módulo de Young E, y coeficiente de Poisson nulo. Se pretende realizar una aproximación de Galerkin, basada en una sola función para cada componente: “y” para aproximar u_x, “yx” para aproximar u_y. Se pide que:

a) Realice un breve comentario acerca de las buenas o malas cualidades de estas funciones a la vista del problema considerado.

b) Calcule la matriz de rigidez. Puede calcular las integrales analíticamente o mediante aproximación de Gauss de un punto. En el último caso, utilice una subdivisión en al menos dos triángulos.

c) Calcule el término de cargas. Realice las integrales analíticamente.

d) Calcule el tensor de tensiones en el punto (L/4, L/4), referido a ejes x,y.

e) Utilizando el diagrama de Mohr, exprese dicho tensor en ejes polares r, q , definidos de la manera habitual.