ELASTICIDAD y RESISTENCIA DE MATERIALES.- 3^er Curso

EXAMEN DE SEPTIEMBRE 1998-99 (materia del 1^er parcial)

Cuestión 1.- Demuestre si son ciertas cada una de las afirmaciones siguientes:

a) En ausencia de efectos debidos a la temperatura, el que cada componente de desplazamiento sea una función armónica y que la divergencia del desplazamiento sea constante, es un conjunto suficiente de condiciones para que no existan fuerzas de volumen (Sugerencia: puede razonar a partir de las ecuaciones de Navier).

b) Afirmación análoga a la anterior, pero existiendo efectos de temperatura.

c) La función de Densidad de Energía de Deformación es definida positiva en un sólido elástico isótropo.

(1+1+1=3 pto)

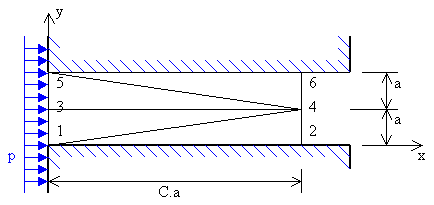
Cuestión 2.- La figura representa una ranura existente en la pared de cierto recipiente, que se supondrá absolutamente rígido en este análisis. La ranura se rellenará desde la izquierda hasta una cierta profundidad (C.a) con resina, la cual, una vez solidificada, tendrá un comportamiento aproximadamente elástico. En condiciones de servicio, existirá una presión p en el interior del recipiente, actuando como se indica. Se ha estimado que uno de los requisitos para que el dispositivo cumpla las funciones previstas, es que el desplazamiento horizontal del punto (C.a, a) no supere el 10% del valor del desplazamiento del extremo izquierdo (0, a).

SE PIDE que calcule el valor mínimo de la constante C para que se satisfaga esta condición. Para ello se utilizará la aproximación en elementos finitos que se muestra, o un subconjunto de ella en caso de que puedan realizarse simplificaciones.

Numere los elementos como desee, pero respete la numeración de nodos. Asuma estado de Deformación Plana en x- y, y considere Módulo de Young = E, y Coeficiente de Poisson nulo.   (4 pto)

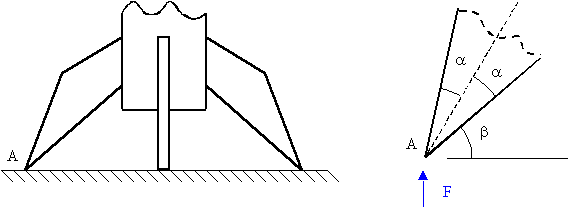
Cuestión 3.- La primera figura muestra un detalle de cierto artefacto apoyado sobre el terreno. Cada una de sus 4 patas es una laja que trabaja en condiciones de tensión plana. Se espera que en cierta región (cercana al vértice A) de la pata, el estado de tensión sea aproximadamente el que se tendría en una "cuña infinita", como muestra la segunda figura. Eventualmente, se piensa utilizar este hecho como comprobación de una solución de tensión en la pata obtenida por ciertos medios. SE PIDE que calcule ese estado de tensión en la cuña infinita, siendo los valores de geometría y carga los mostrados en la segunda figura.    (3 pto)

Nota: Valores de algunas integrales: