ELASTICIDAD y RESISTENCIA DE MATERIALES- TERCER CURSO

EXAMEN ORDINARIO DE JUNIO 1998-99 (parte del primer parcial)

Cuestión 1.- Comente brevemente cada una de las siguientes afirmaciones (se sugiere dedicar menos de 5 minutos a cada una).

a) Un campo de desplazamientos que satisfaga las ecuaciones de Navier y las condiciones de contorno será la solución del problema elástico propuesto.

b) Un campo de tensiones que satisfaga las ecuaciones de Beltrami y Michell y las condiciones de contorno será la solución del problema elástico propuesto si todas las condiciones de contorno están dadas en tensiones.

c) El Criterio de Plastificación de Tresca resulta más conservador (conduce a diseños más seguros) que el de Von-

Mises.

d) Bajo ciertas condiciones, puede ocurrir rotura frágil en un material que en el ensayo de tracción presenta comportamiento dúctil.

e) El principio de los desplazamientos virtuales puede considerarse la base de una familia de métodos de resolución de problemas elásticos.

f) La suma de los elementos de la diagonal del tensor de Cauchy tiene una propiedad matemática particular, y un significado físico concreto.                                                                            (0.5x6=3 ptos.)

 

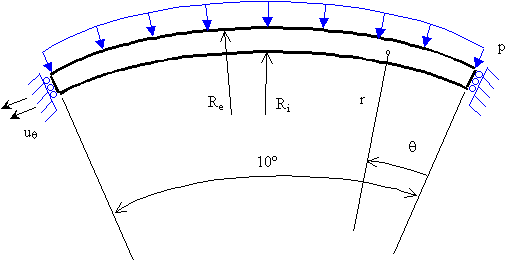
Cuestión 2.- Hace algunos meses, se construyó un puente sencillo entre dos puntos del terreno que distaban 16m, eligiendo para ello una configuración en arco circular que abarca 10° como la que se muestra, de forma que 2R_e x sen 5° = 16m. La sección del arco es rectangular, de ancho 1m, y de canto R_e -R_i = 0.2m. Se pensó que los apoyos podrían mantener el arco en las condiciones que se muestran (desplazamiento normal nulo en los extremos), pero lo cierto es que mediciones recientes

muestran que el extremo izquierdo (q=10º) ha cedido algunos centímetros. Se asumirá que el movimiento circunferencia! de ese extremo es proporcional al radio r , resultando de la interpretación de las mediciones que u_q(q=10º)=(0.05°xprad/180°)r.

Datos adicionales: Módulo de Cortadura = 9x10⁹ kp/m². p=2500 kp/m². El coeficiente de Poisson es tal que el valor del parámetro k de las tablas es k=2.3.

SE PIDE que calcule el campo de tensiones en el arco, y que precise si un punto de r= R_e estará más solicitado (según el criterio de Tresca) que un punto de r= R_i. (Sugerencia: el problema se soluciona en el ámbito de las componentes de función de Airy para problemas axisimétricos de las tablas). (3.5 ptos)

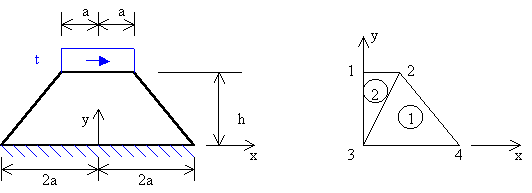
Cuestión 3.- La primera figura representa cierto aspecto del modo de trabajo del freno de una máquina. Se pretende realizar un análisis de Elementos Finitos sobre la mitad del sólido, aprovechando las simetrías o antisimetrías que existen. Para ello se utilizará la discretización de nodos y elementos indicada en la segunda figura. Se pide que realice lo siguiente:

a) En una figura como la segunda, indique las condiciones de contorno en desplazamientos a aplicar en los nodos. Indique esquemáticamente (sin cálculos) qué componentes de la matriz columna de cargas y de la de desplazamientos serán conocidos al principio del análisis, y cuales serán incógnita. Finalmente indique también qué términos de la matriz de rigidez seria innecesario calcular en todo caso, y cuáles sería innecesario calcular si se pretendiese calcular únicamente los desplazamientos nodales.

b) Calcule las componentes del término de cargas que no serán incógnitas de la aproximación, y escriba el término de cargas tal como lo haría si se dispusiese a plantear el sistema global de ecuaciones.

c) Suponga que ahora se pretende obtener analíticamente (no mediante métodos aproximados) la solución del problema. Se sospecha que pudieran surgir dificultades, porque, tal como se planteó la primera figura, la tensión en las esquinas superiores (izda. y dcha.) pudiera no estar representada por un tensor de tensiones con las propiedades usuales. Se pide que aclare si esto último es así o no utilizando razonamientos basados en la representación de Mohr. (1.5+1.5+0.5=3.5 ptos)