INTRODUCCIÓN A LA ELASTICIDAD y RESISTENCIA DE MATERIALES

SEGUNDO CURSO - EXAMEN CONVOCATORIA DE JUNIO 1999

Cuestión 1.- Desarrolle de manera concisa cada uno de los siguientes apartados:

a) Definición e interpretación fisica de los términos del tensor de Cauchy.

b) Concepto de tensor rotación e interpretación (sin demostración) del significado de sus componentes.

c) Demuestre explícitamente si a un campo constante de deformación debe corresponder (o no) un campo también constante de rotación. Por simplicidad, realice esta demostración para estado de deformación plana.

(1.5+ 1 + 1 =3.5 ptos)

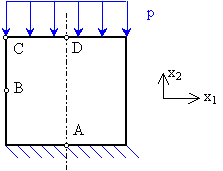
Cuestión 2.- La figura representa un problema bidimensional cuyo material es isótropo. Se pide que:

a) Realice una breve discusión acerca de si el mismo tiene solución analítica sencilla conocida.

b) En un cuadro como el que se muestra (que reproducirá en su examen), rellene con anotaciones tipo "=0", "=+p", "=-p", etc, aquellas casillas en que la magnitud correspondiente sea conocida sin necesidad de realizar ningún cálculo. Aunque no se considera necesario, si quiere comentar alguna casilla puede hacerlo brevemente fuera del cuadro. (Sugerencia: tenga en cuenta tanto las condiciones de contorno como las simetrías que existan).

 

(0.2+0.8= 1 pto)

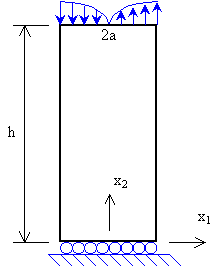
Cuestión 3.- La distribución de carga en la cara superior del sólido bidimensional que se muestra es s₂₂=psen[px₁/(2a)]. Se pide que, basándose en consideraciones sobre el principio de Saint- Venant, deduzca qué forma debe tener sensiblemente la distribución de s₂₂ en la cara inferior cuando h es grande comparado con a, y que calcule la expresión concreta de esa distribución.

Nota: primitivas de algunas funciones:

 § senz dz = -cosz ;   § z sen z dz = -z cosz + senz ;   § sen 2z dz = z/2 -( sen 2z)/4

(1.3+0.7= 2 ptos)

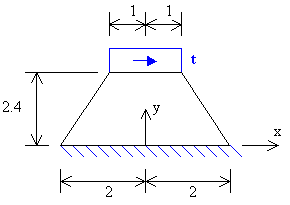
Cuestión 4.- La figura inferior muestra el problema de deformación plana de un sólido sometido a tensión tangencial constante de valor t en su cara superior. Se aprecia que la geometría es simétrica respecto del eje y. El módulo de Young vale E, y el coeficiente de Poisson es nulo.

1. Indique si el problema elástico presenta alguna simetría o antisimetría.

2. Se realizará una aproximación de Galerkin basada en una sola función de aproximación para la componente u_x de desplazamiento, y otra para la componente u_y. Elija razonadamente las funciones más convenientes para ello, entre las posibilidades siguientes:   x² ;    e^y-1 ;   x³y

3. Elegidas las funciones más apropiadas, realice la aproximación de Galerkin y calcule sus parámetros indeterminados. Plantee el análisis en sólo medio sólido si ello es posible. Puede aproximar cada integral en un dominio rectangular o triangular por el valor del integrando en el centro de áreas multiplicado por el área. Opere por unidad de espesor.

4. Calcule y dibuje las distribuciones de tensión s_yy, s_2xy en la base del sólido que resultan de la aproximación.

(0.5+1+1+1=3.5ptos.)