Examen junio 2005
Cuestión 1
Razone y explique el tipo de
condiciones de contorno en tensiones y desplazamientos que deben imponerse en
ejes de simetría y de antisimetría.
Cuestión 2
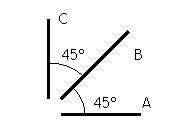 Considere
una galga extensométrica con filamentos A, B, y C a 0, 45 y 90º respectivamente,
como indica la figura. En condiciones de servicio la galga está adherida a la
superficie de un sólido elástico cuyo material es homogéneo e isótropo, de
constantes elásticas conocidas. La medición con este dispositivo ha
proporcionado las deformaciones longitudinales unitarias
eA,
eB,
eC, respectivamente, en las direcciones de los filamentos.
Considere
una galga extensométrica con filamentos A, B, y C a 0, 45 y 90º respectivamente,
como indica la figura. En condiciones de servicio la galga está adherida a la
superficie de un sólido elástico cuyo material es homogéneo e isótropo, de
constantes elásticas conocidas. La medición con este dispositivo ha
proporcionado las deformaciones longitudinales unitarias
eA,
eB,
eC, respectivamente, en las direcciones de los filamentos.
Se pide que para el punto del sólido donde
está colocada la galga, exprese todas las componentes (en tres dimensiones) del
tensor de deformaciones, respecto de unos ejes que Vd. elija. Nota: como
sabe, para poder pegar la galga se requiere una superficie libre del sólido.
Cuestión 3
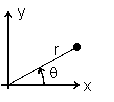 a) Justifique si las
tensiones que derivan de la función de Airy
f=r3 cosq pueden
corresponder a un estado simétrico o antisimétrico de tensiones respecto de
los ejes x o y (orientados según la figura). Nota: no es garantía
suficiente una comprobación solamente en los ejes. Se sugiere que dibuje las
tensiones en puntos simétricos para poder responder a la pregunta.
a) Justifique si las
tensiones que derivan de la función de Airy
f=r3 cosq pueden
corresponder a un estado simétrico o antisimétrico de tensiones respecto de
los ejes x o y (orientados según la figura). Nota: no es garantía
suficiente una comprobación solamente en los ejes. Se sugiere que dibuje las
tensiones en puntos simétricos para poder responder a la pregunta.
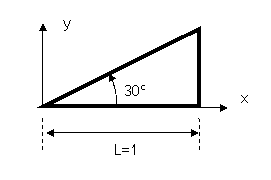 b)
Represente (previo cálculo) las tensiones normal y tangencial en los bordes de
una placa triangular como la de la figura, si su estado de tensión estuviese
descrito por la función de Airy anterior. Acote los valores máximos en la
representación. Utilice obligatoriamente el diagrama de Mohr para realizar las
transformaciones de tensiones que precise. Nota: seguramente le será de ayuda
encontrar la orientación de las direcciones principales con dicho diagrama, como
paso intermedio.
b)
Represente (previo cálculo) las tensiones normal y tangencial en los bordes de
una placa triangular como la de la figura, si su estado de tensión estuviese
descrito por la función de Airy anterior. Acote los valores máximos en la
representación. Utilice obligatoriamente el diagrama de Mohr para realizar las
transformaciones de tensiones que precise. Nota: seguramente le será de ayuda
encontrar la orientación de las direcciones principales con dicho diagrama, como
paso intermedio.
Cuestión 4
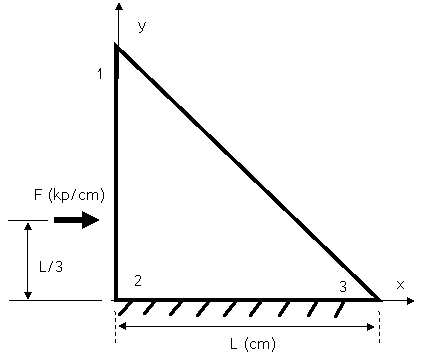 El
triángulo rectángulo de la figura representa esquemáticamente un muro de
sección triangular sobre el cual actúa una carga de valor F, medida en
kilopondios por cada unidad de profundidad del muro. Realice un análisis
mediante el MEF considerando un único elemento coincidente con la geometría de
la sección del muro y con la numeración de nodos indicada. Obtenga cuál es la
energía de deformación total bajo la acción de F.
El
triángulo rectángulo de la figura representa esquemáticamente un muro de
sección triangular sobre el cual actúa una carga de valor F, medida en
kilopondios por cada unidad de profundidad del muro. Realice un análisis
mediante el MEF considerando un único elemento coincidente con la geometría de
la sección del muro y con la numeración de nodos indicada. Obtenga cuál es la
energía de deformación total bajo la acción de F.
Nota: Realice el estudio por
unidad de profundidad. Datos del material: Módulo de Young E, coeficiente de
Poisson nulo.
___________________________________
 Considere
una galga extensométrica con filamentos A, B, y C a 0, 45 y 90º respectivamente,
como indica la figura. En condiciones de servicio la galga está adherida a la
superficie de un sólido elástico cuyo material es homogéneo e isótropo, de
constantes elásticas conocidas. La medición con este dispositivo ha
proporcionado las deformaciones longitudinales unitarias
eA,
eB,
eC, respectivamente, en las direcciones de los filamentos.
Considere
una galga extensométrica con filamentos A, B, y C a 0, 45 y 90º respectivamente,
como indica la figura. En condiciones de servicio la galga está adherida a la
superficie de un sólido elástico cuyo material es homogéneo e isótropo, de
constantes elásticas conocidas. La medición con este dispositivo ha
proporcionado las deformaciones longitudinales unitarias
eA,
eB,
eC, respectivamente, en las direcciones de los filamentos.  a) Justifique si las
tensiones que derivan de la función de Airy
a) Justifique si las
tensiones que derivan de la función de Airy  b)
Represente (previo cálculo) las tensiones normal y tangencial en los bordes de
una placa triangular como la de la figura, si su estado de tensión estuviese
descrito por la función de Airy anterior. Acote los valores máximos en la
representación. Utilice obligatoriamente el diagrama de Mohr para realizar las
transformaciones de tensiones que precise. Nota: seguramente le será de ayuda
encontrar la orientación de las direcciones principales con dicho diagrama, como
paso intermedio.
b)
Represente (previo cálculo) las tensiones normal y tangencial en los bordes de
una placa triangular como la de la figura, si su estado de tensión estuviese
descrito por la función de Airy anterior. Acote los valores máximos en la
representación. Utilice obligatoriamente el diagrama de Mohr para realizar las
transformaciones de tensiones que precise. Nota: seguramente le será de ayuda
encontrar la orientación de las direcciones principales con dicho diagrama, como
paso intermedio.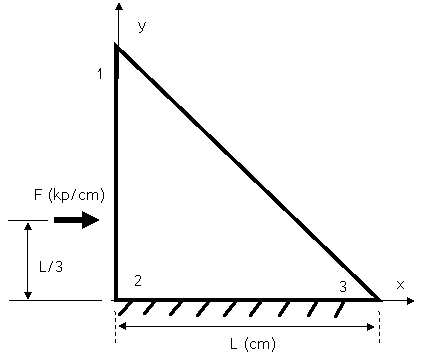 El
triángulo rectángulo de la figura representa esquemáticamente un muro de
sección triangular sobre el cual actúa una carga de valor F, medida en
kilopondios por cada unidad de profundidad del muro. Realice un análisis
mediante el MEF considerando un único elemento coincidente con la geometría de
la sección del muro y con la numeración de nodos indicada. Obtenga cuál es la
energía de deformación total bajo la acción de F.
El
triángulo rectángulo de la figura representa esquemáticamente un muro de
sección triangular sobre el cual actúa una carga de valor F, medida en
kilopondios por cada unidad de profundidad del muro. Realice un análisis
mediante el MEF considerando un único elemento coincidente con la geometría de
la sección del muro y con la numeración de nodos indicada. Obtenga cuál es la
energía de deformación total bajo la acción de F.