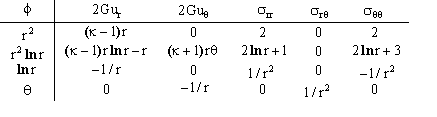
Examen Septiembre 2004

Problema.

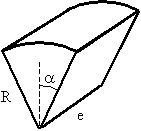
La figura representa una cuña con forma de sector circular, empleada para ser introducida en la grieta de otro sólido (no mostrado), con el objeto de hacer progresar la grieta y fragmentarlo. La cuña tiene radio “R”, profundidad “e” y semiángulo a=10º, y trabaja en condiciones de tensión plana, siendo el módulo de Young E, y n=0. Se aplica una presión radial de valor “p” en su superficie curva.

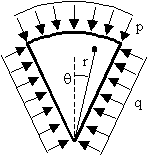
Asuma que las paredes de la grieta ejercen sobre la cuña una presión uniforme de valor “q” (desconocido a priori), como se indica en la segunda figura. Se pide que:

a) Razonando exclusivamente sobre el equilibrio de la cuña, calcule el valor de “q” en función de “p”.

b) Usando las tablas de funciones de Airy adjuntas, calcule el estado de tensión en la cuña.

c) Dibuje la representación de Mohr de tensiones para un punto genérico del contorno curvo (r=R, q cualquiera)

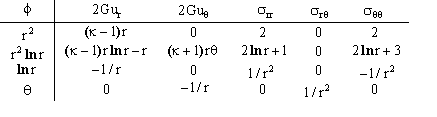
Asuma ahora que tras haber progresado la grieta, la cuña queda con su vértice apoyado en una superficie rígida, como se indica en la tercera figura. Nótese que la presión “q” ya no actúa. Aunque posiblemente conozca otros enfoques para analizar este problema elástico, considere que se realizará una aproximación de Galerkin con las características siguientes:

- dos funciones para cada componente de desplazamiento

- análisis de la mitad derecha de la cuña (sombreada en la figura)

- todas las integrales que deban efectuarse (que serán relativas a la mitad derecha) se aproximarán mediante Cuadratura de Gauss de un punto.

Se pide que:

d) Escoja las funciones para cada componente de desplazamiento de entre las siguientes: xy/R² ;  y/R  ;  xy²/R³  ;  x²y²/R⁴  ; 

e) Calcule la matriz de rigidez de la aproximación. Exprese con al menos dos cifras significativas los coeficientes numéricos que figuren en el resultado.

f) Calcule el término de cargas de la aproximación.

g) Plantee el sistema de ecuaciones de la aproximación, y comente brevemente su estructura (incógnitas...).

_____________________