INTRODUCCIÓN A LA ELASTICIDAD Y RESISTENCIA DE MATERIALES.- 2º curso

Examen septiembre 2003

(Cuestiones 1 y 2 omitidas en esta página)

Cuestión 3.- (3.5 ptos)

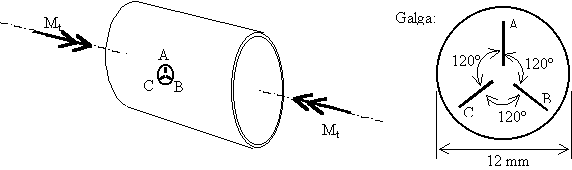
Considere una barra con sección de corona circular, de 500mm de diámetro y 5mm de espesor, que se tratará como “de pequeño espesor”. La misma soporta un momento torsor M_t de 19 Ton ´ m, en el sentido que indica la figura. El material tiene Módulo de Young  2.1´10⁶ Kp/cm², Coeficiente de Poisson  0.3 ,  y su límite elástico es 2400 Kp/cm² . Se pide que:

a)      Calcule el ángulo de giro de la tubería por unidad de longitud, en grados por metro.

b)      Compruebe si habrá plastificación, según el Criterio de Tresca.

c)      En la superficie de la tubería se ha colocado una galga extensométrica como se indica. Sus filamentos están a 120º, y A coincide con la dirección circunferencial. La galga es lo bastante pequeña como para considerar que es aproximadamente plana. Calcule el incremento unitario de longitud de los filamentos A, B y C.

d)   Bajo las mismas consideraciones que en el apartado anterior, calcule el incremento de longitud total (en mm) del perímetro del soporte de la galga, que tiene forma circular de radio 12 mm. 

Observaciones: 1.- Recuerde que en perfiles circulares como el presente, la constante de torsión coincide con el momento polar de inercia. 2.- Evite usar “de memoria” cualquier fórmula de torsión que no sea M_x = GJq. En lugar de ello razone directamente sobre el problema.  3.- Las siguientes integrales pueden serle de utilidad:

Cuestión 4.- (1.5 ptos)

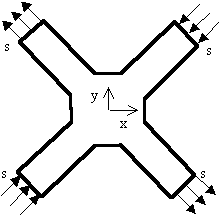
El elemento estructural en forma de aspa de la figura trabaja en condiciones de tensión plana, con tensiones normales de valor absoluto “s” en sus brazos, con los sentidos indicados. Se pide que:

a)      A la vista de los planos de simetría y/o antisimetría que tenga el problema, realice un dibujo de la porción más pequeña del sólido que sería necesario considerar para el análisis del mismo (dibuje también los símbolos para las condiciones de contorno).

b)      Indique el valor de las componentes conocidas de los vectores tensión y desplazamiento en ejes x-y, en los contornos de la porción de sólido aludida. Si en algún contorno no hay valores conocidos pero debe existir alguna relación entre las componentes, exprese dicha relación.

_______________________________________________________________