ELASTICIDAD Y RESISTENCIA DE MATERIALES – 3er curso – plan antiguo
Examen extraordinario de septiembre de 2002. Parte de Elasticidad
Cuestión 1.- (2 ptos) Comente brevemente las incompatibilidades intrínsecas del estado de Tensión plana.
Cuestión 2.- (4 ptos)
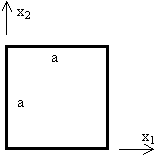
La figura representa una placa cuadrada de dimensiones a´a, que trabaja en condiciones de tensión plana sin fuerzas de volumen. No se representan las tensiones en sus contornos. Se piensa que la distribución de tensiones en la placa pudiera ser de la forma s11=2Cx1x2 ; s22=0 ; s12=-Cx22 ; siendo C una constante. Se pide que:
a) Indique razonadamente si la distribución de tensiones propuesta es físicamente aceptable.
b) Asumiendo la distribución propuesta, represente las tensiones normales y tangenciales en los cuatro bordes de la placa. Acote los valores máximos en cada uno.
c) Utilizando la representación de Mohr, calcule y represente las direcciones y tensiones principales en los vértices superior e inferior derechos (puntos (a,0) y (a,a) ).

Cuestión 3.- (4 ptos)
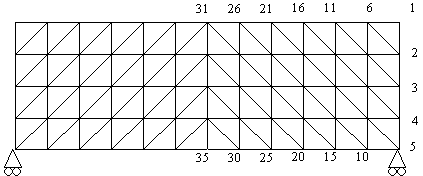
La figura muestra una discretización plana en Elementos Finitos de una viga corta, cuyas dimensiones son 12Lx4L. La numeración de nodos se realiza por columnas, como se indica parcialmente. Existe una carga uniformemente distribuida en la superficie superior, de valor p kgf/m2, dirigida hacia abajo. Considérese espesor unidad. Se pide que:
a) Explique la posibilidad de analizar solamente medio sólido (el derecho), e indique la forma que tendrían el término de cargas, f, y el de desplazamientos, a, en dicho análisis. Calcule el valor de los términos que sea posible calcular a priori.
b) Indique razonadamente, pero sin cálculos, si aprecia que exista alguna relación evidente entre las submatrices K6-1 y K31-26 ; ídem entre K6-1 y K25-20 ;; ídem entre K11-7 y K26-22 ; ídem entre K11-7 y K23-19 ; ; ídem entre K11-6 y K12-7 ; ídem entre K11-7 y K11-17 ; ídem entre K11-17 y K11-8 ;