ELASTICIDAD Y RESISTENCIA DE MATERIALES – 3er Curso.

Examen final ordinario - Junio de 2002 – Parte de Elasticidad

Cuestión 1.- Exponga el criterio de Tresca. Sinopsis: observaciones experimentales que apoyan la verosimilitud del criterio, forma que adopta el criterio, su representación en el espacio de tensiones principales, y su grado de coincidencia con ensayos de “tensión tangencial pura”.   (3 ptos)

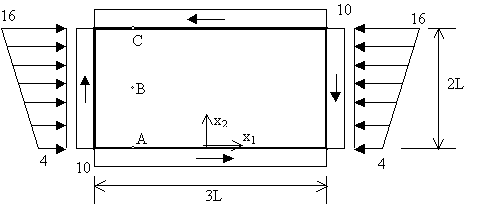
Cuestión 2.- La figura representa una porción de cierto elemento estructural (el alma de una viga), de dimensiones 3L´2L, que trabaja en condiciones de tensión plana. Las tensiones normales en las caras derecha e izquierda evolucionan linealmente con x₂, la tensión normal en las caras superior e inferior es nula, y las tensiones tangenciales en las cuatro caras son constantes, con los sentidos y valores que se indican en cada caso.

Se pide que:

a)       Exprese los términos del tensor de tensiones que son conocidos en cada cara (condiciones de contorno) en función de x₁, x₂.

b)       Obtenga la solución de tensiones en la placa, en los ejes x₁ x₂ (orientación: es claro que un polinomio de Airy con los términos mas típicos de bajo orden puede proporcionar dicha solución; debe identificar la función de Airy, pero si Vd. es capaz de evitar cálculos innecesarios, hágalo).

c)       Trace el diagrama de Mohr para cada uno de los puntos A(-L,0), B(-L,L), y C(-L,2L) indicados.

d)       Usando los diagramas de Mohr, calcule y represente (esto último aproximadamente) la orientación de la dirección principal que tenga menor tensión normal (compresión mayor) en cada uno de los tres puntos.  (4 ptos)

Cuestión 3.- La figura representa la acción de un rodillo (línea de puntos) sobre una base elástica, la cual tiene impedido el movimiento de los bordes que se indican. Asumiendo estado de deformación plana, se pretende realizar una aproximación de Galerkin de la base, con una función para u_x y otra para u_y.

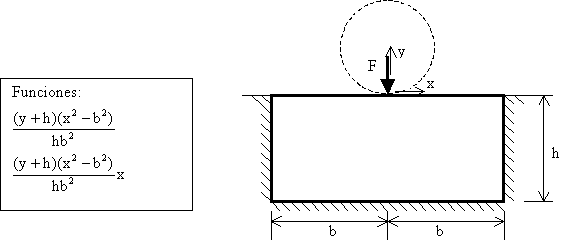
 Se pide que:

a)       De las dos funciones indicadas, escoja razonadamente una para u_x y otra para u_y. Comente los aspectos idóneos o indeseables que aprecie en ellas.

b)       Calcule la(s) matriz (matrices) tipo LN de la aproximación, y exponga cómo obtendría la matriz de rigidez del sistema. Para esto último no realice ninguna integral, ni tampoco productos de matrices (deje indicadas estas operaciones).

c)      Calcule el término de cargas de la aproximación. Exponga la forma que tendría el sistema global de ecuaciones.

(3 ptos)