
INTRODUCCIÓN A LA ELASTICIDAD Y RESISTENCIA DE MATERIALES
EXAMEN SEPTIEMBRE DE 2002 (Continuación)
Cuestión 3.- (1 pto)
Describa brevemente el concepto de superficie de plastificación, así como la evidencia experimental básica asociada a dicho concepto.
Cuestión 4.- (2 ptos)
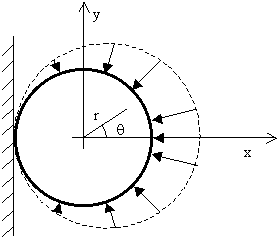
La figura representa un sólido de geometría circular, de radio R, que trabaja en condiciones de deformación plana. Sobre su contorno (r=R) actúa una tensión radial de valor srr= -p cos(q/2), y su extremo izquierdo apoya en una pared rígida como se indica.


a) Basándose en razonamientos de equilibrio, pero sin realizar ningún cálculo, exponga su opinión acerca de cuáles de las siguientes evoluciones de tensiones serían posibles en el plano diametral que pasa por el eje x. Tensión normal: nula / constante / lineal en x anulándose en el extremo izquierdo / ídem anulándose en el extremo derecho. Tensión tangencial: nula / constante / lineal / parabólica.
b) Para las formas de evolución elegidas, calcule el valor concreto de las tensiones en el mencionado plano diametral.
c) Asuma que se pretende realizar una aproximación de Galerkin del problema, usando una sola función para cada componente de desplazamiento. De las dos funciones: (x+R) ; (xy) ; elija razonadamente una para cada componente de desplazamiento, y calcule la matriz de rigidez de la aproximación asumiendo coeficiente de Poisson nulo.
Cuestión 5.- (2 ptos)
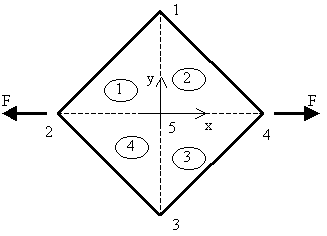
La placa de la figura, de vértices x=±a; y=±a; trabaja en condiciones de tensión plana. Su espesor es e, su módulo de Young vale E y su coeficiente de Poisson es nulo. Se pide calcular el valor de la deformación en los puntos de la placa, utilizando para ello la aproximación en elementos finitos mostrada, o un subconjunto de la misma.