INTRODUCCIÓN A LA ELASTICIDAD Y RESISTENCIA DE MATERIALES

EXAMEN ORDINARIO - JUNIO DE 2002

1) Explique el concepto, propiedades y significado físico del vector deformación, de la deformación normal y de la deformación transversal, así como sus analogías con las magnitudes relativas a la tensión (epígrafe "Otras magnitudes a la deformación" del temario).        (2 ptos)

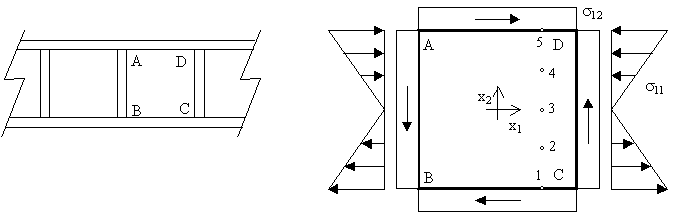
2) La primera figura representa una parte de cierto elemento estructural, llamado viga armada, en el que el rectángulo ABCD es "la porción de alma entre dos rigidizadores transversales", y que a efectos de cálculo es una placa que trabaja en condiciones de tensión plana según se indica en la segunda figura. Las dimensiones de la placa son 1m x 1m, y 1cm de espesor. El límite elástico del material es 2400 kp/cm². SE asume que la tensión tangencial en cada borde de la placa es constante, siendo su resultante 70 Ton, y que las tensiones normales en los bordes izquierdo y derecho varían linealmente como se indica, siendo su momento resultante de 30 Ton x m. No existen tensiones normales en las caras superior e inferior. Se pide que:

a) Obtenga la solución de tensiones para la placa. Orientación: polinomio de Airy de bajo orden (el origen de ejes está en el centro de la placa).

b) Trace los diagramas de Mohr para los puntos numerados del 1 al 5 indicados en la segunda figura, situados a x₁=30cm, x₂=-50, -25, 0, 25 y 50 cm, respectivamente.

c) Compruebe si en alguno de los puntos mencionados existirá plastificación del material según el criterio de Tresca. En caso negativo, indique cual o cuales de ellos están más próximos a plastificar.

d) Obtenga en cada uno de los cinco puntos el valor de la menor tensión principal y la dirección de la normal al plano en que ocurre. Realice una representación aproximada de dichas direcciones.

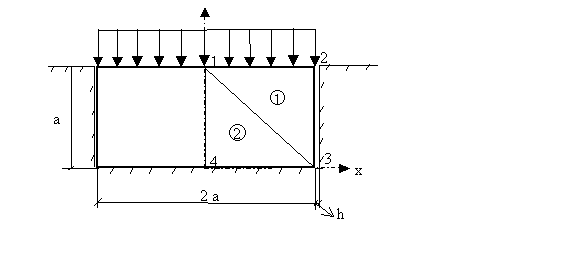
3) Sobre una placa de dimensiones 2a x a (cm) introducida en una ranura rectangular se aplica una presión uniforme de valor p (kp/cm²). Inicialmente (antes de cargar la placa), se cuenta con una holgura entre ésta y la ranura de valor h (cm), tanto en el lateral derecho como en el izquierdo de la misma. Se pretende realizar una aproximación a la solución del problema empleando una discretización en elementos finitos de la mitad derecha de la placa como la indicada en la figura. Se pide:

a) Calcule los términos correspondientes al vector de fuerzas que sean estrictamente necesarios para determinar los parámetros desconocidos de la aproximación. En el caso de que algunas componentes de este vector no pueden ser obtenidas directamente, por intervenir en ellas valores de fuerzas desconocidos a priori, trabaje con términos del tipo X_x, X_y, F_x, F_y                 (3 puntos).

Datos adicionales:

                - Opere por unidad de espesor.

                - El material del que está construida la ranura puede considerarse perfectamente rígido.

                - Tómense como módulo de Young y coeficiente de Poisson para la placa E y n, respectivamente.

                - La matriz que recoge la ley de comportamiento en este problema es:

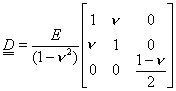
                - El deslizamiento entre los contornos de la placa y la ranura se produce sin rozamiento.

                - El valor de la carga p es tal que los desplazamientos horizontales de la placa hacen que ésta llegue a ajustar perfectamente en la ranura.

b) Indique qué submatrices k_ij elementales habría que calcular para resolver completamente el problema (obtener fuerzas y desplazamientos desconocidos en los nodos). (0,5 puntos)

c) ¿Puede la aproximación en elementos finitos dar la solución exacta para este problema? (0,5 puntos)

d) ¿Qué implicaciones tendría haber considerado n=0 en los cálculos? (0,5 puntos)

e) ¿Cuál sería el valor mínimo de p que sería necesario aplicar para que la placa llegara a cubrir justamente la ranura? (0,5 puntos)