ELASTICIDAD Y RESISTENCIA DE MATERIALES
Examen parcial extraordinario - 9 de marzo de 2002
3er curso, plan antiguo, parte de Elasticidad
Cuestión 1.- 2.5 puntos, 20 min, se recoge en primer lugar.
Interpretación física de los términos del tensor de Cauchy en componentes cartesianas.
Cuestión 2.- 3 puntos, 30 min.
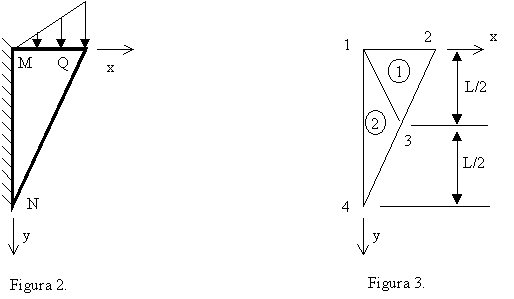
La figura 1. muestra una viga corta (poco esbelta), apoyada en sus extremos y cargada uniformemente como se indica.
a) Indique en un cuadro como el siguiente, que reproducirá en su examen, el valor de las componentes de tensión que sean conocidas a priori como resultado de la observación de las condiciones de contorno y de las simetrías y antisimetrías del problema. Ponga una interrogación (?) en las que no puedan conocerse por dichos medios. Los puntos A, B y C están en la sección media de la viga. (Nota: adviértase la orientación de los ejes).
| A | B | C | D | E | F | |
| sxx | ||||||
| syy | ||||||
| sxy |
b)
A parte
de ciertos detalles constructivos no mostrados, los apoyos de la viga están
constituidos por placas planas triangulares (como la MQN, fig. 1) soldadas a los
pilares. Se pretende realizar el análisis de una de estas placas bajo hipótesis
de tensión plana, con las condiciones de contorno que se muestran en la figura
2. Se pide que dilucide si dichas condiciones de contorno implican alguna
incompatibilidad en el punto Q. (Nota: puede emplear razonamientos basados en el
diagrama de Mohr, en las tensiones principales, etc).
c)
Exponga
brevemente su juicio acerca de la idoneidad de cada uno de los siguientes cuatro
enfoques para el análisis de la placa de la figura 2: 1º: Función de Airy:
polinomio completo de tercer grado. 2º: Función de Airy: coordenadas polares
con origen en uno de los vértices y uso de las tablas manejadas en el curso. 3º:
Aproximación de Galerkin basada en funciones que se anulen en x=0. 4º:
Aproximación de Elementos Finitos

Cuestión 3.- 4.5 puntos, 40 min.
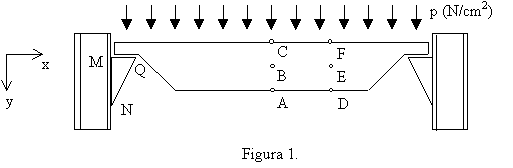
La placa de la figura 2 tiene de dimensiones (L/2)´(L), espesor e, Módulo de Young E, y coeficiente de Poisson nulo. La resultante de la carga triangular vale R (Newtons). Se plantea realizar un análisis de Elementos Finitos según la figura 3. Se pide que:
a) Muestre simbólicamente la estructura de la matriz de rigidez de la aproximación, detallando las aportaciones elementales a cada submatriz. Muestre la estructura del término de desplazamientos y del de cargas, detallando qué componentes serán incógnitas y cuáles serán conocidas (o calculables a priori). Muestre simbólicamente el subsistema de ecuaciones que permitirá calcular el término de desplazamientos. Calcule explícitamente la submatriz f2 del término de cargas, en función de R.
b) Asuma que del cálculo de los desplazamientos nodales resulta a2x = 0.4211R/(Ee); a2y = 1.3684R/(Ee); a3x = -0.1053R/(Ee); a3x = 0.4561R/(Ee). Para asegurar la estabilidad de la placa, es de interés conocer la máxima tensión de compresión y la orientación en la que ocurre. Se pide que los calcule en el centro de áreas del elemento 1, usando el diagrama de Mohr.