ELASTICIDAD Y RESISTENCIA DE MATERIALES

Examen extraordinario - 3 de septiembre de 2001

3^er curso, plan antiguo, parte de Elasticidad

Cuestión 1.- 3.5 puntos. Se realizará en primer lugar. Se recogerá a los 30 min.

Exponga brevemente los fundamentos de la Aproximación de Galerkin y del Método de los Elementos Finitos, aplicados al problema elástico. No penalizará el no incluir la expresión exacta de las matrices de constantes elásticas.

Cuestión 2.- 3.5 puntos. Orientativamente 30 min.

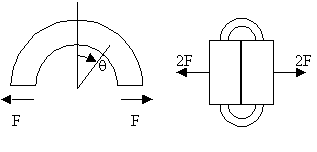
La primera figura muestra un elemento de unión con forma de semicorona circular, de radio interior r_i, y radio exterior r_e, que trabaja en condiciones de tensión plana (considere profundidad unidad en dirección perpendicular al dibujo). Su misión es regular el contacto entre dos bloques conductores de la electricidad, de la manera que indica la segunda figura. Se aprecia que la fuerza resultante en las caras inferiores de la semicorona debe ser F, como indica la primera figura. Se pide que, mediante las tablas de Funciones de Airy, plantee el sistema de ecuaciones de cuya resolución se obtendría una solución de tensiones en la semicorona con las características siguientes: 1.) Respetar que el vector tensión sea nulo en las caras curvas. 2.) Respetar que la resultante sea la "F" indicada, en las caras rectas inferiores. 3.) Que tenga variación en q lo mas sencilla posible.

Cuestión 3.- 3 puntos. Orientativamente 30 min.

En un caso de Deformación Plana, las deformaciones están descritas por e_xx=Axe^y ; e_yy=Bx³(e^y+y) ; e_xy=Cx²y² ; donde x,y son unas coordenadas cartesianas expresadas en determinadas unidades. Se sabe que B>0, y que en el punto x=1, y=0, la tensión tangencial máxima visible en x-y (en planos paralelos a la dirección z) tiene un valor dado M. Se pide que calcule A, B y C, en función de M y de las constantes de Lamé del material (l, G).