Elasticidad y Resistencia de Materiales - Examen extraordinario - 10 de marzo de 2001
Parte de Elasticidad
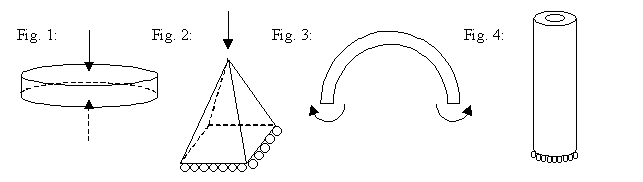
Cuestión 1.- (3 ptos) Considere los siguientes problemas elásticos:
Indique mediante razonamientos breves (que pueden incluir consideraciones sobre las dimensiones relativas, aproximaciones que cabría asumir, etc.) cuales de ellos
serían en principio analizables empleando la Función de Airy.
son axisimétricos, al menos en cuanto a tensiones.

Cuestión 2.- (4.5 ptos) La Figura 5 muestra una placa de unión de un nudo rígido de una estructura metálica, en el cual confluyen dos vigas. Las mismas están soldadas a la placa en un vértice y en su centro (trazos gruesos). Otros elementos no mostrados garantizan que la placa permanecerá plana. Se sabe que cada viga transmite en cada soldadura una fuerza F según se indica. Para el análisis de la placa se opta por el modelo de tensión plana con fuerzas concentradas que muestra la Figura 6. El análisis se realizará mediante una aproximación de Elementos Finitos triangulares (Fig.7). Se Pide que:
a) En virtud de las simetrías y antisimetrías que existan, reduzca el análisis a la porción del sólido mas pequeña que considere posible.
b) Plantee y resuelva la aproximación el E.F. con las simplificaciones del apartado anterior, y las hipótesis adicionales que crea necesario (movimientos como sólido rígido).
c) De las infinitas líneas rectas que pasan por el centro de la placa, encuentre cuáles son las que sufren mayor deformación longitudinal según la solución encontrada, y cuales son los valores de las dichas deformaciones.
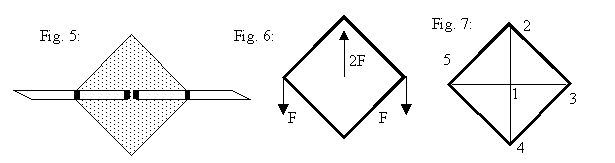
Datos: Módulo de Young = E, Coeficiente de Poisson nulo, espesor de la placa = b, diagonal de la placa cuadrada = 2a.
Cuestión 3.- (2.5ptos) Componentes del vector tensión en función de los términos del tensor de tensiones.