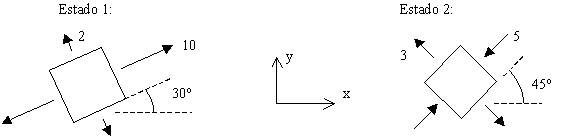
Elasticidad y Resistencia de Materiales - 3er curso (plan antiguo)

EXAMEN FINAL ORDINARIO - PARTE DE ELASTICIDAD - 25 junio 2001

Cuestión 1.- (25 min, 3 ptos) Exponga el criterio de Tresca.

Sinopis: Fundamentos físicos del criterio; representación en el espacio de tensiones principales; caso particular de Tensión Plana. (No se piden conceptos previos, como el de superficie de plastificación general, etc). 

Cuestión 2.- (30 min, 3+1=4 ptos) En la figura, el "Estado 1" muestra las componentes de tensión en un punto de un sólido bidimensional, cuando actúa cierto sistema de cargas en el sólido, digamos sistema 1. Análogamente, el "Estado 2" representa las tensiones en el mismo punto cuando actúa otro sistema de cargas, digamos 2. Se pide que:

a) Calcule y represente mediante un dibujo similar a los de la figura la tensión en ese punto en ejes x-y, cuando actuan simultáneamente los dos sistemas de cargas. Calcule también la t^max en ese caso. Haga obligatoriamente uso del diagrama de Mohr en todos los cálculos de este apartado.

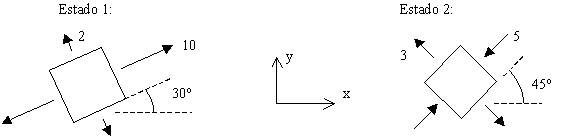
b) Comente brevemente la afirmación siguiente (puede complementar su comentario con una referencia al apartado anterior, tomado a modo de ejemplo):

" Por aplicación del principio de superposición, la t^max en un punto cuando actúan simultáneamente dos sistemas de cargas, es la suma de las t^max correspondientes a cada sistema por separado".

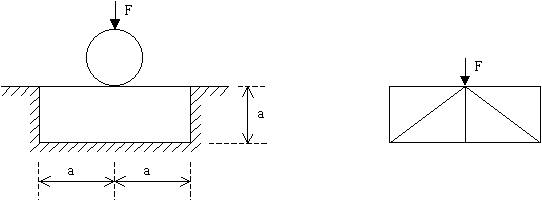
Cuestión 3.- (25 min, 3 ptos) La primera figura representa un dispositivo de apoyo consistente en un material elástico encajado en un medio que se supondrá absolutamente rígido, como se indica. Se asumirá coeficiente de Poisson nulo, Módulo de Young E, y estado de deformación plana con profundidad "e", en la dirección perpendicular al dibujo. Se pide que calcule el movimiento del punto central de la cara superior del material elástico, en el que se transmite la fuerza F a través del rodillo mostrado. Para ello se usará la discretización en 4 Elementos Finitos de la segunda figura, o un subconjunto de ella en caso de que puedan realizarse simplificaciones. Puede numerar los nodos y elementos, y definir los ejes coordenados, como desee.