INTRODUCCIÓN A LA ELASTICIDAD y RESISTENCIA DE MATERIALES

EXAMEN EXTRAORDINARIO - 1 de SEPTIEMBRE de 2001

Cuestión 1.- (Teórica. 3.5 puntos; orientativamente 1 hora) Nota previa: base todos los razonamientos de esta cuestión en el enfoque gráfico de la Representación de Mohr, aplicado al diagrama degenerado en consideración. Los razonamientos basados en otros métodos se valorarán menos.

Considere el caso de un estado de tensiones en un punto p tal que la ecuación característica tenga una raíz doble. En particular, asuma que la misma tiene valor mayor que la raíz sencilla, y por lo tanto es s_I = s_II > s_III. Se pide que:

a)      Indique brevemente, sin demostración, la particularidad mas destacada de las direcciones principales en un estado tensional como el propuesto.

b)      De entre las siguientes, elija razonadamente la afirmación que le parezca acertada, e indique la localización del (/de los) plano(/s) aludido(/s):

·          Existe un solo plano que pasa por P con un valor dado de s (con s_III < s < s_I ).

·          Existen dos únicos planos que pasan por P con un valor dado de s (con s_III < s < s_I ).

·          Existen infinitos planos que pasan por p con un valor dado de s (con s_III < s < s_I ).

c)      De entre las siguientes, elija razonadamente la afirmación que le parezca acertada:

·          El valor de s (con s_III < s < s_I ), determina el valor de t. O lo que es lo mismo: no es posible encontrar planos con tensión normal s que presenten una diversidad de valores de t.

·          El valor de t (con t < (s_I-s_III)/2), determina el valor de s. O lo que es lo mismo: no es posible encontrar planos con tensión tangencial t que presenten una diversidad de valores de s.

d)      Comente brevemente cada una de las afirmaciones siguientes:

·          El estado de tensión planteado coincide con el que se define en los "problemas planos".

·          En el estado de tensión planteado, es posible establecer un convenio de signos para t.

·          El manejo gráfico del Diagrama de Mohr para el caso propuesto es completamente análogo al de los "problemas planos".

Cuestión 2.- (3.5 puntos; orientativamente 1 hora). Nota previa: advierta que es posible realizar de modo independiente los apartados b y c.

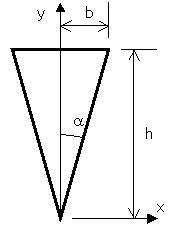
La cuña de la figura, en la que es b<h, está sometida a un estado de tensiones descrito por la función de Airy f=Ax²y. Se pide que:

a)      Indique si las tensiones que derivan de f constituirán un estado simétrico de tensiones respecto del eje y.

b)     Represente (previo cálculo) las componentes normal y tangencial de tensión en todo el contorno de la cuña.

c)      Juzgue cual es el punto más solicitado del sólido, y obtenga el máximo valor de A al que se podría llegar sin plastificación, según los criterios de Tresca y de Von-Mises. Asuma estado de tensión plana, y límite elástico de valor s_e.

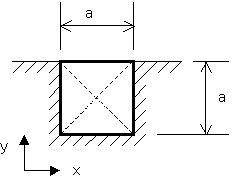
Cuestión 3.- (3 puntos; orientativamente 50 min.) Notas previas: Asuma coeficiente de Poisson nulo. No utilice posibles simetrías del problema. Opere por unidad de espesor. Puede numerar nodos y elementos como desee. Puede colocar el origen de ejes donde desee. Puede aproximar cualquier integral que necesite realizar mediante cuadratura de Gauss de 1 punto.

 La figura representa el problema bidimensional de un medio elástico pegado a un recipiente que se supone rígido. El conjunto se encuentra girando con velocidad angular w respecto de un eje paralelo a y. a una gran distancia R a la derecha, de forma que la fuerza de por unidad de volumen en el medio elástico es constante, de valor rRw², dirigida hacia la izquierda. Se pide que calcule el desplazamiento del punto medio del sólido. usando la aproximación en 4 Elementos Finitos que se indica en línea de puntos.