EXAMEN ORDINARIO - 11 junio de 2001 – 2º curso
INTRODUCCIÓN A LA Elasticidad y Resistencia de Materiales
No se utilizará ningún tipo de calculadora ni formulario en la realización del examen.
Cuestión 1.- ( 2 ptos, 25 min).
a) Enumere y comente brevemente las hipótesis básicas de la Teoría de la Elasticidad.
b) Enumere y comente brevemente los modelos de comportamiento de materiales que conozca.
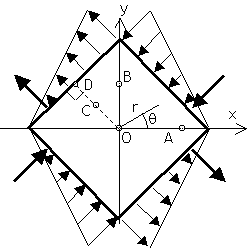
Cuestión 2.- (2 ptos, 25 min). La placa de la figura es cuadrada, formando sus contornos rectos 45º con los ejes x, e y. Se considerará que el punto O no se mueve, y que su entorno no gira en promedio. En cada lado, la carga distribuida crece linealmente desde cero hasta el mismo valor absoluto "p", y las cargas concentradas, del mismo módulo, "F", se aplican en puntos simétricos respecto de x,y. Se pide que complete un cuadro como el siguiente, que reproducirá en su examen. Pondrá en cada casilla el valor de la magnitud correspondiente en cada punto (O, A, B, C y D), en los casos en que dicho valor pueda conocerse mediante observación de las condiciones de contorno indicadas, y las simetrías o antisimetrías del problema. Pondrá un signo de interrogación (?) en caso contrario.

| ux | uy | exx | exy | eyy | sxx | sxy | syy | ur | uq | srr | srq | sqq | |
| O | |||||||||||||
| A | |||||||||||||
| B | |||||||||||||
| C | |||||||||||||
| D |
Cuestión 3.- (3 ptos, 45 min). La figura muestra el problema plano de una viga corta de espesor e, canto 2a y longitud L, con una fuerza aplicada en el punto (L,0), y movimientos impedidos en el contorno x=0. El coeficiente de Poisson del material es cero, y el Módulo de Young, E. Se pretende realizar una aproximación de Galerkin con dos funciones para ux, elegidas entre x/L, xy/L2, x2y/L3, xy2/L3, y otras dos funciones para uy, elegidas entre y2/L2, x3/L3, x2y/L3, xy2/L3. Se pide que:
a) Elija las dos funciones más apropiadas para cada componente de desplazamiento.
b) Plantee el sistema de ecuaciones de cuya resolución obtendría el valor de las incógnitas de la aproximación (no se pide que resuelva dicho sistema, pero sí que concrete los valores de K y de f).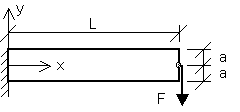
Nota: Valor de algunas integrales en el dominio L´2a´e en cuestión (si necesita alguna otra integral, deberá calcularla Vd. mismo):
| Función: | y2 | x3 | x4 | xy2 | x2y2 |
| Integral: | 2eLa3/3 | eaL4/2 | 2eaL5/ | ea3L2/3 | 2ea3L3/9 |
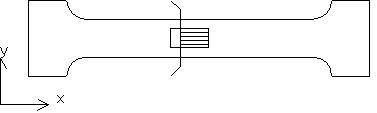
Cuestión 4.- (3 ptos, 45 min). La primera figura muestra una probeta plana para ensayo de tracción. Se sabe que el coeficiente de Poisson del material es 0.3. La deformación longitudinal se medirá con una galga extensométrica unidireccional, como se indica. Se pide que responda a los siguientes apartados:
a) El no colocar la galga correctamente alineada con la dirección x de la probeta, producirá cierto error en la medición de la deformación longitudinal. Calcule en función de q la expresión y el signo de dicho error, siendo q el ángulo entre x y los filamentos de la galga. Utilice el diagrama de Mohr para deformaciones en este apartado, obligatoriamente. (Nota: suponga en este aparado que la galga mediría correctamente si se colocase bien, es decir, no tenga en cuenta aquí las consideraciones del apartado b).